Class 9 Maths notes for Areas of Parallelograms & triangles
Welcome to Class 9 Maths chapter 9 Areas of Parallelograms & triangles notes.The topics in this page are Area of figure,Figure on the same base and between same parallels,Parallelogram on same base and between same parallel,Area of Parallelogram, and Triangles and Parallelogram.This is according to CBSE and the NCERT textbook. If you like the study material, feel free to share the link as much as possible.
Area of a figure is a number (in some unit) associated with the part of the plane enclosed by that figure.
Area can be measured in various ways
(1) Area by Counting Squares: We can also put the shape on a grid and count the number of squares of unit area
(2) Approximate Area by Counting Squares: Sometimes the squares don't match the shape exactly, but we can get an "approximate" answer
using more than half a square counts as 1 and less than half a square counts as 0
(3) Using a formula (when possible) : It can be calculated using mathematics formula. We can find formula for various figures
(4) Area of Difficult Shapes: We can sometimes break a shape up into two or more simpler shapes for which we know the formula
(5) Area by Adding Up Triangles : We can try to divide the area into multiples traingle and then calculating the area
Properties of Area
(1) Two congruent figures have same area
What are congruents figures
Two figures are congruent, if they're exactly the same shape, and they're exactly the same size. They may appear different because one is shifted or rotated a certain way, but they're still the same shape, and all the sides of one are the same length as the corresponding sides of the other.
(2) If two figure have same area, they are not necessary congruent
(3) If a planar region formed by a figure T is made up of two non-overlapping planar regions
Formed by figures P and Q, then ar (T) = ar (P) + ar (Q), where ar (X) denotes the area of
Figure X.
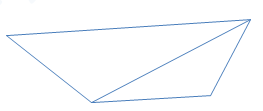
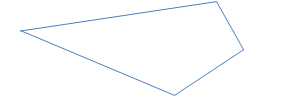
Figure on the same base and between same parallels
Two figures are said to be on the same base and between the same parallels, if they have a common base (side) and the vertices, (or the vertex) opposite to
the common base of each figure lies on a line parallel to the base.
In the above figure triangle and parallelogram are on the same base and between same parallel
Parallelogram on same base and between same parallel
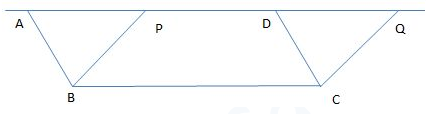
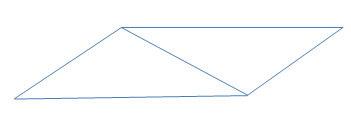
Parallelograms on the same base (or equal bases) and between the same parallels are equal in area.
Area of Parallelogram ABCD= Area of Parallelogram PBCQ
Formula for Area of Parallelogram
A parallelogram is a 4-sided shape formed by two pairs of parallel lines. Opposite sides are equal in length and opposite angles are equal in measure.
To find the area of a parallelogram, multiply the base by the height. The formula is:
Area of parallelogram is equal base multiplied by Height
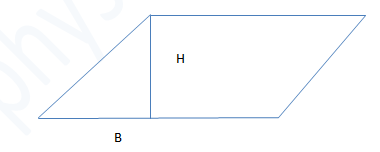
The base and height of a parallelogram must be perpendicular. However, the lateral sides of a parallelogram are not perpendicular to the base.
Thus, a line is drawn to represent the height.
Parallelograms on the same base (or equal bases) and having equal areas lie between the same parallel
How to Find the Area of parallelogram
(1) First step is to convert base and height into same unit. i,e if base is given in cm and height is given in m, Then we need to first convert base and height into either
meter or cm
(2)Calculate the area using the formula
(3) If the area is given and either height or base is missing,then we can find using b=A/h or h=A/b
Examples:
(1) Find the area of a parallelogram with a base of 2 inches and a height of 10 inches. Solution:
A = (2 in).(10 in)
A = 20 in2
(2)The area of a parallelogram is 12 square centimeters and the base is 4 centimeters. Find the height
Solution: Let h be the height then
12 = (4 ).h
h = 3 cm
Triangles and Parallelogram
(a) If a parallelogram and a triangle are on the same base and between the same parallels, then area of the triangle is half the area of parallelogram
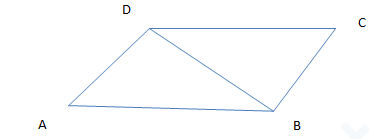
Area of triangle ADB= 1/2 X Area of parallelogram ABCD
(b) Triangles on the same base (or equal bases) and between the same parallels are equal in area
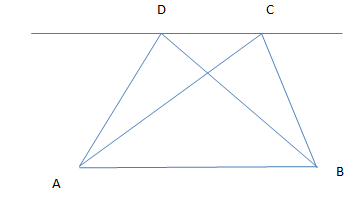
Area of triangle ABD=Area of triangle ACB
Area of Triangle
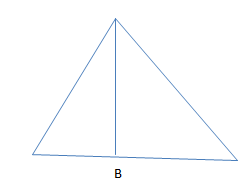
(1) Area of triangle is given by
A=1/2 BXH
(2) Triangles on the same base (or equal bases) and having equal areas lie between the same
Parallels
How the Parallelogram area is calculated
The area is defined as the number of square units in the figure. We know for a rectangle ,it is given as
A=L X B
Now let us consider the parallelogram given below
Here B is the Base of the parallelogram
and H is the height of the parallelogram
Let us move the traingle part as shown in figure to the other side
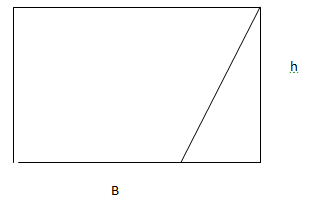
Which is a rectangle of Area =BH
Summary
Here is the summary of Area of Parallelogram And Triangle Notes for Class 9 Maths
Two figures are said to be on the same base and between the same parallels, if they have a common base (side) and the vertices, (or the vertex) opposite to the common base of each figure lie on a line parallel to the base
Parallelograms on the same base (or equal bases) and between the same parallels are equal in area
Area of a parallelogram is defined as product of its base and the corresponding altitude.
Parallelograms on the same base (or equal bases) and having equal areas lie between the same parallels
Triangles on the same base (or equal bases) and between the same parallels are equal in area
Area of a triangle is defined as half the product of its base and the corresponding altitude
