Triangles Class 9 Maths notes

Welcome to Class 9 Maths chapter 7 Triangles notes.The topics in this page are What is congruence, Triangle Congruence ,How to Prove the congurence of Two Triangle and Inequality of Triangle along with examples, and questions and answers .This is according to CBSE and the NCERT textbook. If you like the study material, feel free to share the link as much as possible.

• What is Congruence
• Triangle Congruence
• Properties of Congurent trianngles
• Different Criterion for Congruence of the triangles
• How to Prove the congurence of Two Triangle
• Inequality of Triangle
• Important defination for Triangles
• Solved Examples

What is Congruence

• In geometry, two figures or objects are congruent if they have the same shape and size, or if one has the same shape and size as the mirror image of the other.
• A combination of rigid motions, namely a translation, a rotation, and a reflection is also permitted in Congruence. Translation means sliding,Rotation means turning and Reflection means Flipping. If two figures can be overlapped using translation,rotation or reflection then they are congruence
• It has come from Latin word congruere "agree, correspond with"

What is the difference between Congruence and Similarity?

Why do we need to Learn it?

• We need to learn congruence in order to identify and describe many Congruent object in real life. It may be some sculpture, some old monuments,
• In Pyramid, all the three triangular surface are Congruent.AROUND 2600 B.C., construction of the Great Pyramid of Khufu began. It took the ancient Egyptians about 30 years to transform 6.5 million tons of stone into a pyramid with a square base and four congruent triangular faces
• We need several identical shirts button ,various factory part and many numerous objects. All these need the concept of Congruence
  
  
  

  Congruence

  Two Geometric figure are said to be congruence if they are exactly same size and shape
  
  • Symbol used is ≅
  • Two angles are congruent if they are equal
  • Two circle are congruent if they have equal radii
  • Two squares are congruent if the sides are equal
  • Two line segments are congruent if they have equal length
  
  

  Triangle Congruence

  • Two triangles are congruent if three sides and three angles of one triangle is congruent to the corresponding sides and angles of the other
    
  • Corresponding sides are equal $AB=DE \; , \; BC=EF \; ,\; AC=DF$
  • Corresponding angles are equal
    
  • We write this as
    $ \Delta ABC \cong \Delta DEF$
  • The above six equalities are between the corresponding parts of the two congruent triangles. In short form this is called C.P.C.T
  • We should keep the letters in correct order on both sides

  Properties of Congruent triangles

  
  (1) Reflexive Property of Congruent Triangle: Every Triangle is Congruent to itself
  $ \Delta ABC \cong \Delta ABC$
  (2) Commutative or symmetric property of Congruent Triangle:
  if $ \Delta ABC \cong \Delta DEF$ then $ \Delta DEF \cong \Delta ABC$
  
  (3) Transitive Property Of Congruent Triangle
  if $ \Delta ABC \cong \Delta DEF$ and $ \Delta DEF \cong \Delta LKM$ then $\Delta ABC \cong \Delta LKM$
  
  Since Congruence relation satisfy Reflexive ,symmetric and Transitive ,it is an equivalence relation
  

  Different Criterion for Congruence of the triangles

  SAS Congruence (AXIOM)

  

  ASA Congruence (Theorem)

  

  AAS Congruence (Theorem)

  

  SSS Congruence (Theorem)

  

  RHS Congruence (Theorem)

  
  
  Caveat
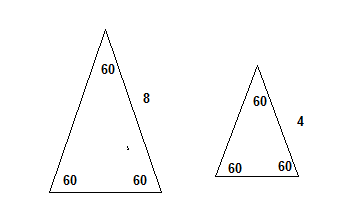
  1) AAA( Angle Angle Angle) is not the right condition to Prove congruence.
  The below two equilateral triangles have same angles 60⁰.But they are not congruent
  
  
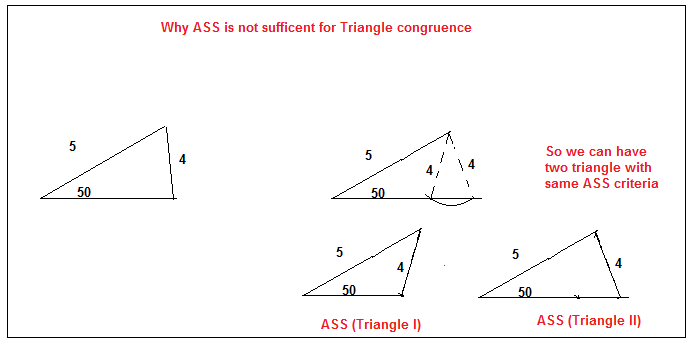
  2) SSA and ASS is also not the right condition to Prove congruence.
  The below figure explain why it is not the right condition
  
  

  How to Prove the congruence of Two Triangle

  1. We have already studied that two triangles are Congruent when all the sides and all the angles are equal. But we don't need to prove all these while solving the Problem
     
  2. We just need to prove the congruence using the different criterion like SSS,ASA,SAS,RHS,AAS
     
  3. Don't use AAA
     
  4. Use the theorem learn in previous Geometry chapter like vertically opposite angles,alternate interior angles,corresponding angles
     
  5. Write down the corresponding angles and corresponding sides carefully
     
  6. We need to be careful with the labelling when our Triangles are in different positions
     

  Inequality of Triangle

  (1) In a triangle angle opposite to longer side is larger
  
  (2) In a triangle side opposite to larger angle is larger
  (3) The sum of any two sides of the triangle is greater than the third side
  In triangle ABC
  $AB +BC > AC$
  (4) Difference of any two sides of triangle is less than the third side
  $AC-AB < BC$ where $AC > AB$
  
  

  Important definition for Triangles

  Median

  A line Segment joining the corner of the triangle to the mid point of the opposite side of the triangle. All the median of the triangle passes through the same point
  

  Centroid

  Point of intersection of the three median of the triangle is called the centroid of the triangle. The centroid divides each of the median in the ration of 2:1
  

  Altitude

  A line Segment from the corner of the triangle and perpendicular to the opposite side of the triangle. All the altitude of the triangle passes through the same point
  

  Ortho-centre

  Point of intersection of the three altitude of the triangle is called the orthocenter of the triangle.
  

  In-center

  All the angle bisector of the triangle passes through same point .It is called in-center.
  

  Circumcenter

  The perpendicular bisector of the sides of the triangles passes through same point. It is called circumcenter
  

  Solved Example

  Question 1
  
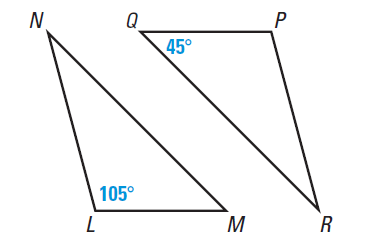
  Here $LMN \cong PQR$
  (i)What is the measure of the angles P,M,R,N?
  (ii)Write down the corresponding Congruent sides?
  Solution:
  By Congruence, All the corresponding angles and corresponding sides are equal
  $LMN \cong PQR$
  Steps to find the All the corresponding angles and corresponding sides
  (i) For angles, The First alphabet on right hand side corresponds to First alphabet on Left hand side,Similarly second and third alphabet
  So $\angle L= \angle P$
  $ \angle M=\angle Q$
  $\angle N=\angle R$
  Now $\angle L=105^0$
  $\angle Q=45$, So $\angle M=45^0$
  $ \angle P=105^0$
  Now $\angle R$ can be found from the theorem
  "Sum of the all the angles in a triangle is 180⁰"
  So $\angle R=180-105-45=30^0$
  $\angle N=30^0$
  (ii) For sides,The first two alphabet on right hand side corresponds to First two alphabet on Left hand side,Similarly 2,3 and 3,1
  $LM=PQ$
  $MN=QR$
  $LN=PR$
  
  Question 2
  
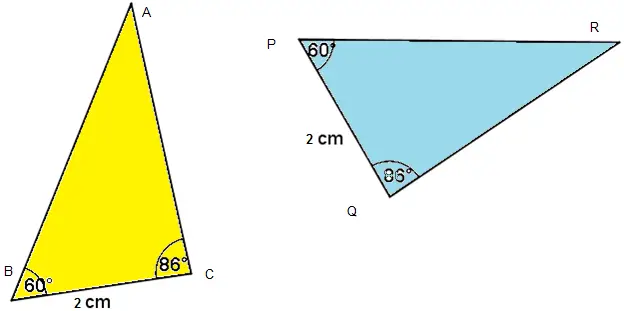
  Please check if these triangle are congruent and then provide the congruent relation
  Solution:
  Here Two angles and side between them is equal,So by ASA Criterion, these triangle are congruent
  The congruency can be written as by simply equating the angles
  $ \Delta ABC \cong \Delta RPQ$
  

  Quiz Time

  Question 1 which of these below is correct criteria for Congruency ?
  
  A.ASA
  B.AAA
  C.SSS
  D.SSA
  Question 2 which of these below is correct criteria for Congruency ?
  
  A. ASA
  B. AAA
  C. SSS
  D. Not a congruency rule
  Question 3 Which of these is true in below figure
  
  A. $\angle A =\angle N$
  B. $\angle C =\angle M$
  C. $\angle A =\angle M$
  D. None of these
  Question 4 which is of these is correct congruence relation for above figure
  A. $ \Delta ABC \cong \Delta LMN$
  B. $ \Delta ABC \cong \Delta NML$
  C. $ \Delta ABC \cong \Delta MNL$
  D. $ \Delta ABC \cong \Delta MLN$
  Question 5 Are the triangle in below figure congruent ?
  
  A. True
  B. False
  Question 6 Which of following cannot be the sides of the triangle?
  A. 3,4,5
  B. 10,5,4
  C. 3.5,4.5,4
  D. none of these
  

  View Results
  
  

  Summary

  Here is Congruent triangles Class 9 Maths notes summary
  • Two Geometric figure are said to be congruence if they are exactly same size and shape
  • Two triangles are congruent if three sides and three angles of one triangle is congruent to the corresponding sides and angles of the other
  • The two triangles are congruent if the two sides and the included angle of one triangle are equal to the two sides and the included angle of the other triangle (SAS Congruence Rule).
  • The two triangles are congruent if two angles and the included side of one triangle equal two angles and the included side of the other triangle (ASA Congruence Rule).
  • The two triangles are congruent if two angles and one side of one triangle equal two angles and the corresponding side of the other triangle (AAS Congruence Rule).
  • Sum of any two sides of the triangle is greater than the third side
  
  Also Read
  

  ---

  • Notes
    • Triangles Class 9 Notes
    • triangles Class 9 Cheatsheet
  • Assignments
    • NCERT Solution Triangles Class 9 Exercise 7.1
    • Congruent triangles class 9 worksheet with answers
    • Triangles class 9 extra questions

  ---

  
  

  ---

  
  Class 9 Maths Class 9 Science