Welcome to Class 9 Maths chapter 4 Linear Equations in two Variable notes.The topics in this page are What is Linear equations, Linear equations Solutions and Graphical Representation of Linear equation in one and two variables along with examples, and questions and answers .This is according to CBSE and the NCERT textbook. If you like the study material, feel free to share the link as much as possible.
Table of Content
What is Linear equations
- A linear equation is an algebraic equation in which each term is either a constant or the product of a constant and (the first power of) a single variable. Linear equations can have one or more variables
Example
$ax+b=0$, $a \neq 0$
a and b are constant
$ax+by+c=0$ , $a \neq 0$ and $b \neq 0$
a,b,c are constants
- In Linear equation ,No variable is raised to a power greater than 1 or used as the denominator of a fraction.
So, $ax^2 +b=0$ is not a linear equation
Similary $ \frac {a}{x}+b=0$ is not a linear equation
- Linear equations are straight lines when plotted on Cartesian plane
Linear equations Solutions
S.no
|
Type of equation
|
Mathematical representation
|
Solutions
|
1
|
Linear equation in one Variable
|
$ax+b=0 \; , \; a \neq 0 $
a and b are real number
|
One solution
|
2
|
Linear equation in two Variables
|
$ax+by+c=0 \; , \; a \neq 0 \; and \; b \neq 0$
i,e a and b both should not be zero.
This condition is often represented as $a^2 + b^2 \ne 0$
a, b and c are real number
|
Infinite solution possible
|
3
|
Linear equation in three Variables
|
$ax+by+cz+d=0 \; , \; a \neq 0 \;, \; b \neq 0 \; and \; c \neq 0$
i,e a , b and c all should not be zero.
This condition is often represented as $a^2 + b^2 +c^2 \ne 0$
a, b, c, d are real number
|
Infinite solution possible
|
Question 1.
Find four different solutions of the equation $x + 2y = 6$.
Solution
We can get many solutions of the linear equation by just picking a value of your choice for x
Here We can find the solutions by putting x=0,1,2,3
For x= 0
$0 +2y=6$ or $2y=6$ or y=3
So (0,3) is a solution
For x= 1
$1 +2y=6$ or $2y=5$ or y=2.5
So (1,2.5) is a solution
For x= 2
$2 +2y=6$ or $2y=4$ or y=2
So (2,2) is a solution
For x= 3
$3 +2y=6$ or $2y=3$ or y=1.5
So (3,1.5) is a solution
Hence the four solutions are
(0,3) , (1,2.5) ,(2,2) and (3,1.5)
Question 1.
Draw the graph of each of the equations given below. Also, find the co-ordinates of the point where the graph cuts the co-ordinates axis:
(a) 2x + y = 6
(b) 3x + 2y + 6 = 0
Solution
To draw the graph, we need at least two solutions of the equation
We can get two points by putting x=0 and y=0. And then draw the graph. Corrdinates will be given by (x,0) and (0,y)
(a)
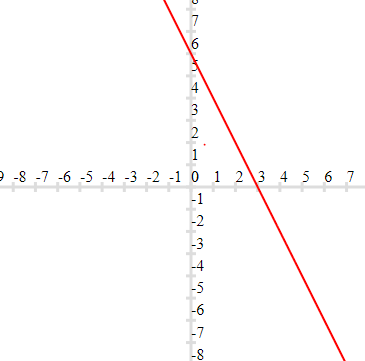
Coordinates are (3,0) and (0,6)
(b)
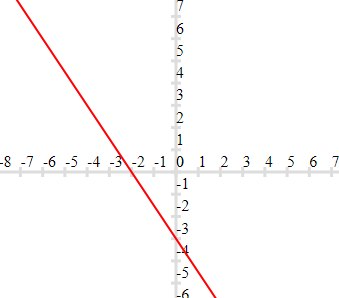
Coordinates are (-2,0) and (0,-3)
Question 2.
Any point on the y-axis is of the form
(a) (x, 0)
(b) (x, y)
(c) (0, y)
(d) ( y, y)
Solution
Answer is C
Question 3.
At what point does the graph of the linear equation x + y = 5 meet a line which is parallel to the y-axis, at a distance 2 units from the origin and in the
positive direction of x-axis.
Solution
The coordinates of the points lying on the line parallel to the y-axis, at a distance 2 units from the origin and in the positive direction of the x-axis are of the form (2, a).
Putting x = 2, y = a in the equation x + y = 5, we get a = 3. Thus, the required point is (2, 3).


