

Consider a sphere to be assembled by number of infinitesimally thin spherical shells. Suppose at any instant r be the radius of the sphere and now we add a charged shell of radius dr to this sphere of radius r. This process continues till the radius of sphere becomes equal to R. Now, charge on sphere of radius r having volume charge density $\rho$ is
$q= \frac {4}{3} \pi r^3 \rho$
And amount of charge on the shell of thickness dq is
$dq= 4 \pi r^2 \rho dr$
Work done in adding charge q to sphere containing charge q is
dW=Potential of sphere of radius r x charge contained in the shell. Thus,
$dW=\frac{\frac{4}{3}\pi r^3\rho}{4\pi\epsilon_0r} \times 4\pi r^2\rho dr$
or
$dW=\fra
c{4}{3}\frac{\pi\rho^2r^4dr}{\epsilon_0}$
Total work done in assembling a sphere of radius R would be
W=\int_{0}^{R}{\frac{4}{3}\frac{\pi\rho^2r^4dr}{\varepsilon_0}=\frac{4\pi\rho^2r^5}{15\varepsilon_0}}
If Q is the total amount of charge on the sphere then,
$Q=\frac{4}{3} \pi R^3 \rho$
$\rho=\frac{3Q}{4\pi R^3}$
Putting this value of $\rho$ in equation (1) we get
$W=\frac{4\pi R^5}{15\varepsilon_0}\left(\frac{3Q}{4\pi R^3}\right)^2$
This work is stored as potential energy of the system, hence
$U=\frac{3}{5}\frac{Q^2}{4\pi\varepsilon_0R}$
Thus, energy required to assemble a sphere of charge is directly proportional to the square of total charge and inversely proportional to the radius of the sphere
Suppose the charges on the sphere of radius r and R are $Q_1$ and $Q_2$ respectively. Then total charge,
$Q=Q_1+Q_2$
Let $\sigma$ be the surface charge density then,
$\sigma=\frac{Q_1}{4\pi r^2}=\frac{Q_2}{4\pi R^2}$
or
$\frac{Q_1}{Q_2}=\frac{r^2}{R^2}$
$\frac{Q_1}{Q_2}+1=\frac{r^2}{R^2}+1$
$\frac{Q_1+Q_2}{Q_2}=\frac{Q}{Q_2}=\frac{r^2+R^2}{R^2}$
$Q_2=Q\left(\frac{R^2}{r^2+R^2}\right)$
Similarly we can find
$Q_1=Q\left(\frac{r^2}{r^2+R^2}\right)$
Suppose at common centre, potentials due to charge $Q_1$ and $Q_2$ are $V_1$ and $V_2$. Then,
$V_1=\frac{Q_1}{4\pi\varepsilon_0r}=\frac{Qr}{4\pi\varepsilon_0r(r^2+R^2)}$
and
$V_2=\frac{Q_2}{4\pi\varepsilon_0R}=\frac{QR}{4\pi\varepsilon_0R(r^2+R^2)}$
$\therefore V=V_1+V_2=\frac{Q}{4\pi\varepsilon_0}\left(\frac{R+r}{r^2+R^2}\right)$
(a) We have
$E_x=-\frac{\partial V}{\partial x} =-160x$
$E_y=-\frac{\partial V}{\partial y}=-120y$
$E_z=-\frac{\partial V}{\partial z}=0$
So Electric Field vector
=(-160x)i+(-120y) j
(b)Electric Field vector at point P==320i-480j
(c) Value of potential at point P is
$V=80x^2 + 60y^2 = 320+960 = 1280$ V
Potential at the centre of circular loop is given by
$= (\frac{1}{4\pi\varepsilon_0})(\frac{q}{r})$
Where r is the radius of circular loop
Potential at a distance x from the centre of the loop is given by
$=(\frac{1}{4\pi\varepsilon_0})(\frac{q}{\sqrt{r^2+x^2}})$
Now Let takes A and B are respective centres of the two circular loop
Potential at A=Potential at A due to loop I + Potential due to Loop II
$V_A=(\frac{1}{4\pi\varepsilon_0})(\frac{q}{r}) + (\frac{1}{4\pi\varepsilon_0})(\frac{q}{\sqrt{r^2+x^2}})$
Now here x=.12m r=.09 and $q=10^{-6}$ C
Substituting these values
$V_A=2.4 \times 10^5$ V
Potential at B=Potential at B due to loop I + Potential due to Loop II
$V_B=(\frac{1}{4\pi\varepsilon_0})(\frac{q}{r}) + (\frac{1}{4\pi\varepsilon_0})(\frac{q}{\sqrt{r^2+x^2}})$
Now here x=.12m r=.05 and $q=10^{-6}$ C
So $V_B=1.7 \times 10^5$ V
So $V_A- V_B=7 \times 10^4$ V
For the charge q to be in equilibrium, the charges -Q should be at equal distance from it in opposite direction. For equilibrium of Charge Q, the sum of forces acting on it should also be zero. Let assume r be the distance between the charges
So
$\frac {Q^2}{4r^2} - \frac {Qq}{r^2}=0$
Hence q=Q/4
It does not depend on the distance r.
The equilibrium position is not stable. Since when charge -Q is shifted along left by a distance x, the force of attraction from positive charge
$F_1=\frac{Q^2}{4(a+x)^2}$
The force of repulsion from negative charge
$F_2=\frac{Q^2}{(2a+x)^2}$
It is clear that $F_2 > F_1$
So the charge Q will move still farther from the position of equilibrium
Similarly, if the charge -Q is move toward right the force of attraction will be more then Force of repulsion and it will move toward the centre.
Now if the charge q is moved right or left, the force of attraction on one side will more than the force of attraction of other side, so it will return to equilibrium position.

Consider a small elemental length dx having charge dq
Then $dq=(\frac {Q}{L})dx$.
Now potential due to this small charge at point P
$dV=K(\frac{Qdx}{Lx})$
Where $K=\frac{1}{4\pi\varepsilon_0}$
Potential at P due to total charge Q
$ V =\int_{r-l}^{r}\frac{KQdx}{Lx} = (\frac{KQ}{L})ln (\frac{r}{r-L})$
Electric Field is defined as
$E=-\frac{dV}{dr}=\frac{d}{dr} (\frac{KQ}{L})ln (\frac{r}{r-L})$
$=\frac{KQ}{Lr(r-L)}$
In an electric field say E potential at any point near the dipole is
$V=V_d-V_E$
Where $V_d$ is the potential at point P due to the dipole and $V_E$ is the potential at point P due to the uniform electric field.
If r is the position vector of point P from the centre of the dipole then
$V_d=\frac{k\mathrm{\mathbf{p}.} \hat{\mathrm{\mathbf{r}}}}{r^2}=\frac{k\mathrm{\mathbf{p}.\mathbf{r}} }{r^3}$
Now potential at P due to uniform electric field is
$V=\mathrm{\mathbf{E}.\mathbf{r}}$
$=\frac{k\mathrm{\mathbf{p}.\mathbf{r}} }{r^3} - \mathrm{\mathbf{E}.\mathbf{r}}= \frac {kpr \cos \theta}{r^3}-E r cos \theta$
$\theta$ is the angle which dipole axis makes with the uniform electric field. Thus,
$V=\left(\frac{kp}{r^3}-E\right)r \cos{\theta}$
For equipotential surface quantity in the brackets must be equal to zero.
$\Rightarrow\left(\frac{kp}{r^3}-E\right)=0$
or,
$=\left(\frac{kp}{E}\right)^{1/3}$
where,$k=\frac{1}{4\pi\varepsilon_0}$
is a constant.
Electric potential due to electric dipole is given by
$V=\frac{1}{4\pi\varepsilon_0}\frac{pcos{\theta}}{r^2}$
(1) when point lies on the axis of the dipole
$V=\frac{1}{4\pi\varepsilon_0}\frac{p{cos0}^0}{r^2}=\frac{1}{4\pi\varepsilon_0}\frac{p}{r^2}$
$\frac{1}{4\pi\varepsilon_0}=9\times10^9$
Now putting the values of p and r in above equation we find
V=1.26 Volts
On axis of dipole electric field is given by
$E=\frac{2p}{4\pi\varepsilon_0r^3}$
Substituting in the required given values we find
E=2.52 V/m
(2) For points lying on the perpendicular bisector of the dipole $\theta=90^0$ thus,
$V=\frac{1}{4\pi\varepsilon_0}\frac{pcos{9}0^0}{r^2}=0$
And
$E=\frac{2p}{4\pi\varepsilon_0r^3}$
Substituting in the required given values we find
E=2.52 V/m
Let r be the radius of each small drop and q be the amount of charge on each one of them. Potential at the surface of each drop is
$V=\frac{q}{4\pi\varepsilon_0r}$ Volt --- (1)
There are total 15 drops. Volume of the large drop would be same as the volume of all small drops. If R is the radius of the larger drop then,
$\frac{4}{3}\pi R^3=15\times\frac{4}{3}\pi r^3$
$ R=\left(15\right)^{1/3}r$
Charge on the large drop is Q=15q therefore potential of large drop is
$V'=\frac{15q}{4\pi\varepsilon_0(15)^{1/3}r}$ Volt
$=\frac{15V}{(15)^{1/3}}$
Given that V=5 Volt substituting the value in above equation and calculating we find
V'=30.4Volts
Potential energy is given by
$U= \frac {1}{4 \pi \epsilon _0}[ \frac {-q^2}{d+x} + \frac {-q^2}{d-x}]$
or
$U= \frac {-q^2}{4 \pi \epsilon _0}\frac {2d}{d^2 -x^2}$
Sketching the graph between P.E. v/s x
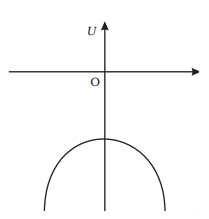
$\frac {dU}{dx}= \frac {-2dq^2}{4 \pi \epsilon _0}\frac {2x}{(d^2 -x^2)^2}$
Now
$\frac {dU}{dx}=0$ at x=0
x = 0 is an equilibrium point.
$U_0= \frac {2q^2}{4 \pi \epsilon _0 d}$
Now doing double differentiation and checking the point of maxima and minima
$\frac {d^2U}{dx^2} = \frac {-2dq^2}{4 \pi \epsilon _0} [ \frac {2}{(d^2 -x^2)^2} - \frac {8x^2}{(d^2 -x^2)^3}]$
or
$=(\frac {-2dq^2}{4 \pi \epsilon _0} )(\frac {1}{(d^2 -x^2)^3}) [2 (d^2 -x^2)^2 -8x^2]$
At x=0, we have
$\frac {d^2U}{dx^2} = (\frac {-2dq^2}{4 \pi \epsilon _0} )(\frac {1}{d^6})(2d^2) $
The above quantity is less than zero, so this is the point of maxima and hence unstable equlibrium