Equipotential surface

Equipotential surfaces

• Surface over which the electric potential is same everywhere is called an equipotential surface.
  
• Equipotential surfaces are graphical way to represent potential distribution in an electric field.
  
• We can draw equipotential surfaces through a space having electric field.
  
• For a positive charge , electric field would be in radially outward direction and the equipotential surfaces would be concentric spheres with centres at the charge as shown below in the figure.
  
  
• Since electric potential remains same everywhere on an equipotential surface from this it follows that PE of a charged body is same at all points on this surface.This shows that work done in moving a charged body between two points on an equipotential surface would be zero.
  
• At every point on equipotential surface electric field lines are perpendicular to the surface. This is because potential gradient along any direction parallel to the surface is zero i.e.,
  $E=- \frac {dV}{dr}=0$
  so component of electric Field parallel to equipotential surface is zero.
  
• This can also be proved as below
  "If the field were not normal to the equipotential surface, it would have non-zero component along the surface. To move a unit test charge against the direction of the component of the field, work would have to be done. But this is in contradiction to the definition of an equipotential surface there is no potential difference between any two points on the surface and no work is required to move a test charge on the surface.The electric field must, therefore, be normal to the equipotential surface at every point"
  
• Two equipotential surfaces can never intersect. If two equipotential surfaces could intersect, then at the point of intersection there would be two values of electric potential which is not possible.
• For a uniform electric field say along x -axis, the equipotential surfaces are planes normal to the x-axis i.e y-z plane
  
  
• The spacing between equipotential surfaces enables us to identify regions of a strong and weak field as $E=- \frac {dV}{dr}$
• More examples of equipotential surfaces
  Equipotential surfaces of a dipole
  
  Equipotential surfaces of two identical positive charges
  
  

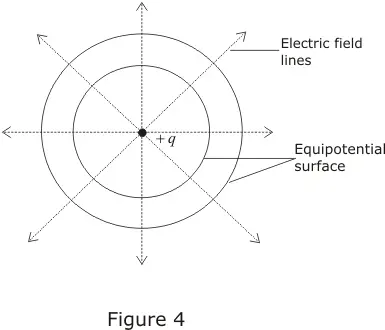
Question 1
Equipotential surfaces
(a) are closer in regions of large electric fields compared to regions of lower electric fields.
(b) will be more crowded near sharp edges of a conductor.
(c) will be more crowded near regions of large charge densities.
(d) will always be equally spaced
Solution
(a), (b), (c)

Question 2
Which of the following is not the property of equipotential surfaces?
(a)They do not cross each other
(b)They are concentric spheres for uniform electric field
(c)Rate of change of potential with difference on them is zero
(d)They can be imaginary spheres
Solution
(a), (c), (d) are correct

Question 3
The below figure shows some equipotential lines distributed in space.

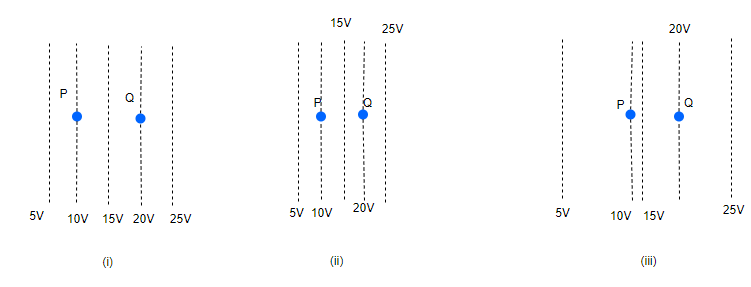
A charged object is moved from point P to point Q.
(a) The work done in Fig. (i) is the greatest.
(b) The work done in Fig. (ii) is least.
(c) The work done is the same in Fig. (i), Fig. (ii) and Fig. (iii).
(d) The work done in Fig. (iii) is greater than Fig. (ii)but equal to that in Fig. (i)
Solution
(c) as work done depends on ends points only

• Notes
  • Electric potential energy
  • Electric Potential
  • Relation between electric fields and electric potential
  • Equipotential surfaces
  • Potential due to an electric dipole
  • Potential energy of dipole placed in uniform electric field
• Assignment
  • Electric Potential MCQ
  • Electric Potential Problems