

(i) Since this is polynomial function, it is continous
(ii) we have
$h(t)= -\frac {7}{2} t^2 + \frac {13}{2} t + 1$
$h'(t) = -7t+ \frac {13}{2}$
For maxima
$-7t+ \frac {13}{2}=0$
or t=13/14 sec
Given
The volume of the tank = $250 \; m^3$
Now since this square base
$x^2 \times h = 250$
Solving for h:
$h = \frac {250}{ x^2}$
(i) Total cost C of digging the tank in terms of x:
Now, the cost of digging the tank increases with depth, and for the whole tank, it is $40,000 h^2$.
Cost of digging (C) = $40000 h^2$
Substituting the value of h from above
$C = 40000 \times \frac {62500}{x^4}$
$C = 25 \times 10^8 \frac {1}{x^4}$
(ii) Derivative dC/dx:
$\frac {dC}{dx} =\frac {d}{dx} (25 \times 10^8 \frac {1}{x^4})$
$= -10^10 \times \frac {1}{x^5}$
(iii) For Minima
$\frac {dC}{dx}=0$
$-10^10 \times \frac {1}{x^5}=0$
So there is no value of x that minimizes the cost. This means that the cost C keeps decreasing as x increases without bound.
So, there is no minimum cost for digging the tank; it will keep getting cheaper as the tank's side x increases.
(iv) Since derivative is negative , it is a decreasing function
Since $-1 \geq sin 2x \geq 1$
Maximum Value is 6 and Minimum value is 4
Median is given by
$M= \frac {\sqrt 3}{2} a$
Now
$\frac {dM}{dt} =\frac {\sqrt 3}{2} \frac {da}{dt}$
Now $\frac {dM}{dt}=2 \sqrt 3$
Therefore
$\frac {da}{dt}=4 $ cm/s
Let x and y be the two numbers
$x+ y=5$
Now
$C= x^3 + y^3 $
This can be written in one variable as
$C=x^3 + (5-x)^3 $
$\frac {dC}{dx} = 3x^2 - 3(5-x)^2$
Now for Minima
$\frac {dC}{dx}=0$
$3x^2 - 3(5-x)^2=0$
or x = 5/2
Now
$\frac {d^2C}{dx^2} = 6x + 6(5-x)$
At x=5/2
$\frac {d^2C}{dx^2} = 30$
Hence it is least
Now y = 5-x=5/2
Now
$x^2 + y^2 = 25/2$
Let the radius be \( r \) and the area \( A \). We know \( A = \pi r^2 \).
Differentiating both sides with respect to time \( t \), we get \( \frac{dA}{dt} = 2\pi r \frac{dr}{dt} \).
Given \( \frac{dr}{dt} = 2 \) cm/s and \( r = 5 \) cm, we find
\( \frac{dA}{dt} = 2\pi \times 5 \times 2 = 20\pi \) cm2/s.
First, find the derivative:
\( f'(x) = 6x^2 - 30x + 36 \).
Set \( f'(x) = 0 \) to find critical points:
\( 6x^2 - 30x + 36 = 0 \).
Solving this, \( x = 2 \) or \( x = 3 \).
To determine the maxima, check the second derivative or use the first derivative test.
Here, \( f''(x) = 12x - 30 \). Since \( f''(2) > 0 \) and \( f''(3) < 0 \), the function has a maximum at \( x = 3 \).
The maximum value is \( f(3) = 2(3)^3 - 15(3)^2 + 36(3) + 1 = 28 \).
First, find the derivative: \( y' = 2x - 4 \).
At \( x = 2 \), the slope of the tangent is \( y'(2) = 2(2) - 4 = 0 \).
The y-coordinate at this point is \( y(2) = 2^2 - 4(2) + 3 = -1 \).
The equation of the tangent is \( y = mx + c \).
Since the slope \( m = 0 \) and it passes through \( (2, -1) \),
\( -1 = 0(2) + c \), so \( c = -1 \).
Thus, the equation is \( y = -1 \).
First, find the derivative:
\( f'(x) = 3x^2 - 6x - 9 \).
Set \( f'(x) = 0 \) to find critical points:
\( 3x^2 - 6x - 9 = 0 \).
Solving this, we get \( x = -1 \) and \( x = 3 \).
Test intervals around these points to determine sign
The function is increasing on \( (-\infty, -1) \) and \( (3, \infty) \), and decreasing on \( (-1, 3) \).
Let \( y = x^{1/3} \).
At \( x = 8 \), \( y = 2 \).
The differential \( dy \) is given by \( dy = \frac{1}{3}x^{-2/3} dx \).
With \( dx = 0.1 \) (since we are approximating \( \sqrt[3]{8.1} \)), \( dy = \frac{1}{3} \cdot 8^{-2/3} \cdot 0.1 \approx 0.0125 \). Thus, \( \sqrt[3]{8.1} \approx 2 + 0.0125 = 2.0125 \).
Let ABCD is a rectangle incribed and 2p and 2q being the side as shown below
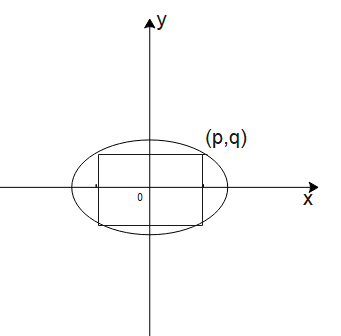
As (p,q) lies on the ellipse
$\frac {p^2}{a^2} + \frac {q^2}{b^2}=1$
or
$q^2=b^2(1-\frac {p^2}{a^2})$
Now Area of the rectangle is given by
$A = 2p \times 2q $
$A= 4pq$
or
$A^2 = 16 p^2 q^2$
Or
$A^2= 16 p^2 b^2(1-\frac {p^2}{a^2})$
$A^2=16b^2(p^2-\frac {p^4}{a^2})$
Now
$\frac {dA^2}{dp} = 16b^2(2p-\frac {4p^3}{a^2})$
for A to be max, $A^2$ is to max
So,
$\frac {dA^2}{dp} =0$
$16b^2(2p-\frac {4p^3}{a^2})=0$
or $p^2=a^2/2$
Now
$\frac {d^2A^2}{dp^2} = 16b^2(2-\frac {12p^2}{a^2})$
Substituting the values of p
$\frac {d^2A^2}{dp^2} < 0$
Hence
Area is maximum at this value
$A=4pq$
$=4 \frac {a}{\sqrt 2} \times b^2(1-\frac {1}{2})= 2ab$
Any point on the parabola is $(at^2 ,2at)$
Now distance is given by
$D^2= (at^2 -11a)^2 + (2at)^2$
$D^2 = a^2t^4 -18a^2t^2 + 121a^2$
Now D to be min, $L=D^2$ is to max
$L= a^2t^4 -18a^2t^2 + 121a^2$
$\frac {dL}{dt} = 4a^2t^3 - 36a^2 t $
For minimum of L
$\frac {dL}{dt}=0$
$4a^2t^3 - 36a^2 t=0 $
or t=0,3,-3
Now $\frac {d^2L}{dt^2} = 12a^2t^2 - 36a^2$
for t=0, $\frac {d^2L}{dt^2} < 0$, hence maxima
for t=3,-3 $\frac {d^2L}{dt^2} > 0$, hence minima
Hence we have two points where the distance is minimum, the cordinates are
(9a ,6a) and (9a ,-6a)
- The slope of the tangent to \( y = x^3 - 3x + 2 \) is given by the derivative \( y' = 3x^2 - 3 \).
- At \( x = 2 \), \( y' = 3(2)^2 - 3 = 12 - 3 = 9 \).
The derivative of \( y = \sin x \) is \( \frac{dy}{dx} = \cos x \).
Answer is (a) \( \cos x \)
The derivative of \( f(x) = e^{2x} \) is obtained by using the chain rule. It is \( f'(x) = 2e^{2x} \).
Answer is (a) \( 2e^{2x} \)
The slope of the normal to the curve \( y = x^2 \) at \( x = 1 \) is the negative reciprocal of the derivative at that point.
The derivative \( y' = 2x \), so at \( x = 1 \), \( y' = 2 \). The slope of the normal is \( -1/2 \).
The equation of the normal is \( y - 1 = -\frac{1}{2}(x - 1) \), which simplifies to \( y + x = 2 \).
The second derivative of \( y = \ln(x) \) is \( \frac{d^2y}{dx^2} = -\frac{1}{x^2} \).
To find the maximum value of \( f(x) = -x^2 + 4x - 3 \), first find the derivative and set it to zero to find critical points.
\( f'(x) = -2x + 4 \). Setting \( f'(x) = 0 \) gives \( x = 2 \).
The maximum value is \( f(2) = -(2)^2 + 4(2) - 3 = -4 + 8 - 3 = 1 \).
The function \( f(x) = x^3 - 3x^2 + 4 \) has a horizontal tangent when its derivative is zero.
\( f'(x) = 3x^2 - 6x \). Setting \( f'(x) = 0 \) gives \( x(3x - 6) = 0 \). Thus, \( x = 0 \) or \( x = 2 \).
- The rate of change of the area \( A \) of a circle with respect to its radius \( r \) is given by \( \frac{dA}{dr} \). Since \( A = \pi r^2 \), \( \frac{dA}{dr} = 2\pi r \).
we know that
$-1 \leq sinx \leq 1$
Also sinx obtained its minimum value of -1 at $\frac {3\pi}{2}$
So absolute minimum value is -2
f(x)= x -sin x
f'(x) =1 -cos x
for decreasing
1 -cos x < 0
or 1< cos x
Which is not possible
Hence (d)