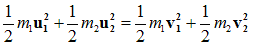Elastic Collisions

Elastic Collisions

• Elastic collision is a collision where the both kinetic energy and Linear Momentum is conserved
• Coefficient of restitution for the Elastic collision is 1
• Elastic collision can be further divided into head on collision (i.e collision in one dimension) and opaque collision (i.e collision in two dimension)
• If the initial velocities and final velocities of both the bodies are along the same straight line, then it is called a one-dimensional collision, or head-on collision. In the case of small spherical bodies, this is possible if the direction of travel of body 1 passes through the centre of body 2 which is at rest.
• the collision is two dimensional, where the initial velocities and the final velocities lie in a plane
• Lets study about these two elastic collision in one dimension and two dimension in further details

Head on elastic collision of two particles

• Consider two particles whose masses are m₁ and m₂ respectively and they collide each other with velocity u₁ and u₂ and after collision their velocities become v₁ and v₂ respectively.
  
• Collision between these two particles is head on elastic collision. From law of conservation of momentum we have
  m₁u₁ + m₂u₂ = m₁v₁ + m₂v₂                      (1)
  and from law of conservation of kinetic energy for elastic collision we have
                       (2)
  rearranging equation 1 and 2 we get
  m₁(u₁-v₁)= m₂(v₂-u₂)                     (3)
  and
  
  dividing equation 4 by 3 we get
  u₁ + v₁ = u₂ + v₂
  u₂ - u₁ = -(v₂ - v₁)                     (5)
  where (u₂ - u₁) is the Relative Velocity of second particle w.r.t. first particle before collision and (v₂ - v₁) is the relative velocity of second particle w.r.t. first after collision.
  
• From equation 5 we come to know taht in a perfectly elastic collision the magnitude of relative velocity remain unchanged but its direction is reversed. With the help of above equations we can find the values of v₂ and v₁ , so from equation 5
  v₁ = v₂ - u₁ + u₂                     (6)
  v₂ = v₁ + u₁ - u₂                     (7)
  Now putting the value of v₁ from equation 6 in equation 3 we get
  m₁(u₁ - v₂ + u₁ - u₂) = m₂(v₂ - u₂)
  On solving the above equation we get value of v₂ as
  
  
• Similarly putting the value of v₂ from equation 7 in equation 3 we get
  
  
• Total kinetic energy of particles before collision is
  
  and total K.E. of particles after collision is
  
  
• Ratio of initial and final K.E. is
  
  
• Special cases
  Case I: When the mass of both the particles are equal i.e., m₁ = m₂ then from equation 8 and 9 , v₂=u₁ and v₁=u₂. Thus if two bodies of equal masses suffer head on elastic collision then the particles will exchange their velocities. Exchange of momentum between two particles suffering head on elastic collision is maximum when mass of both the particles is same.

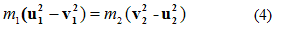
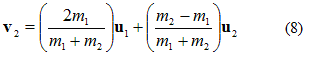
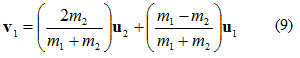
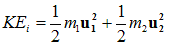
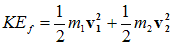
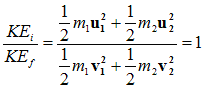
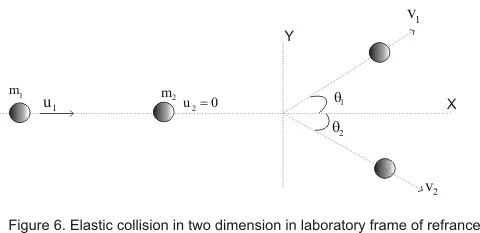
  Case II: when the target particle is at rest i,e u₂=0
  From equation (8) and (9)

  
  
  

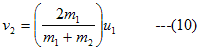
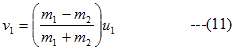
  Hence some part of the KE which is transformed into second particle would be

  
  
  when m₁=m₂,then in this condition v₀=0 and v₂=u₁ and part of the KE transferred would be
  =1

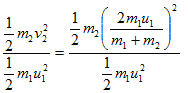
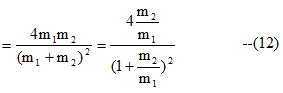
  Therefore after collisom first particle moving with initial velocity u₁ would come to rest and the second particle which was at rest would start moving with the velocity of first particle.Hence in this case when m₁=m₂ transfer of energy is 100%.if m₁ > m₂ or
  m₁ < m₂ ,then energy transformation is not 100%

  
  Case III:
  if m₂ >>>> m₁ and u₂=0 then from equation (10) and (11)
  v₁ ≅ -u₁ and v₂=0                     (13)
  For example when a ball thrown upwards collide with earth
  
  Case IV:
  if m₁ >>>> m₂ and u₂=0 then from equation (10) and (11)
  v₁ ≅ u₁ and v₂=2u₁                     (14)

  Therefore when a heavy particle collide with a very light particle at rest ,then the heavy particle keeps on moving with the same velocity and the light particle come in motion with a velocity double that of heavy particle

(15) Deflection of an moving particle by a particle at rest during perfectly elastic collision in two dimension

• Let m₁ and m₂ be the two mass particle in a laboratory frame of refrence and m₁ collide with m₂ which is initailly is at rest.Let the velocity of mass m₁ before collison be u₁ and after the collison it moves with a velocity v₁ and is delfected by the angle θ₁ withs its incident direction and
  m₂ after the collision moves with the velocity v₂ and it is deflected by an angle θ₂ with its incident direction
  
  
  
• From law of conservation of linear momentum ,for components along x-axis
  m₁u₁=m₁v₁cosθ₁ +m₂v₂cosθ₂ ---(1)
  For components along y-axis
  0=m₁v₁sinθ₁ -m₂v₂sinθ₂ --(2)
  And from law of conservation of energy
  (1/2)m₁u₁²=(1/2)m₁v₁²+(1/2)m₂v₂² ---(3)

• Analysing above equations we come to know that we have to find values of four unknown quantities v₁,v₂,θ₁,θ₂ with the help of above three equations which is not possible. So we cannot predict the variable as they are four of them . However if we measure any one variable ,then other variable can be uniquely determined from the above equation

Also Read

---

• Notes
  • Center of Mass
  • Velocity of centre of mass
  • Acceleration of centre of mass
  • Kinetic energy of the system of particles
  • Linear Momentum of System of particles
  • Center Of Mass Frame of Reference
• Assignments
  • Center of Mass Problems with Solutions
  • Center of mass Problems for class 11

---

---

Latest Updates Sound Class 8 Science Quiz

---

Limits Class 11 MCQ

---

Circles in Conic Sections Class 11 MCQ

---

Plant Kingdom free NEET mock tests

---

The Living World free NEET mock tests

---