Laws of Motion and friction Numericals

Given
$x=at^{3/2} -bt + c$ ---(1)
(a)We know that
$ a=\frac{d^2x}{dt^2}$
So differentiating the equation (1) twice w.r.t to time
$a=\frac{3at^{-1/2}}{4}$
(b) Now force is given by
$F=ma$
So $F=\frac{3mat^{-1/2}}{4}$
(c) At t=1
$F=\frac {3ma}{4} \ N$
(d) From equation 1, it is clear that
$at^{3/2}$ has dimension L
So dimension of a will be $LT^{-3/2}$

Net force on the object
F_net = F₁ + F₂ + F₃
F_net = (20i + 30j) +(22i -10j) +(6i+4j) = 48i + 24j
Now , Acceleration is given by
a = F_net/m = 6i+3j

(b) Now equation of motion
$\mathrm{s\ }=\mathrm{\ u}t+\frac{1}{2}at^2$
Here, u =0 and t= 4 sec
so
s = (1/2) (6i+3j) *16 = 48i+24j

(c) F_net =48i + 24j
Magnitude=$\left(48^2+24^2\right)^{1/2} =53.65$ N Direction =${tan}^{-1}{2}$
(d) F_net =48i + 24j
Now
F_net + F₄ =0
F₄=- F_net = -(48i + 24j) N

Let a be the acceleration of the system
Let $f_1$ be the contact force between A and B
Let $f_2$ be the contact force between B and C
Let's draw free body diagram for each object

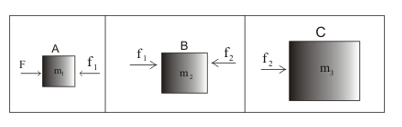
For object A
$F- f_1 = m_1a$ ---(1)
For object B
$f_1 - f_2 =m_2 a$ ---(2)
For object C
$f_2 =m_3 a$ ---(3)
Adding 1 ,2 and 3 we get
$a=\frac{F}{m_1+m_2+m_3}$
Substituting the value in 1 and 3 ,we get
$f_1 =\frac{(m_2+m_3)F}{m_1+m_2+m_3}$
$f_2 = \frac{m_3F}{m_1+m_2+m_3}$

Let take $a_1$ as the acceleration of block $m_1$ towards left. This will also be the acceleration of Pulley B because the strings length is constant.
Similarly, as the strings length is constant over pulley B, magnitude of Acceleration of block $m_2$ will be same as acceleration of block $m_3$ with respect to pulley B. Let assume that acceleration to be $a_2$.
Then Acceleration of Block $m_2$ wrt to ground will be = $a_1 - a_2$ (downward)
Then Acceleration of Block $m_3$ wrt to ground will be = $a_1 + a_2$ (downward).
Let take $T_1$ be the tension in upper string and $T_2$ be the tension in the lower strings

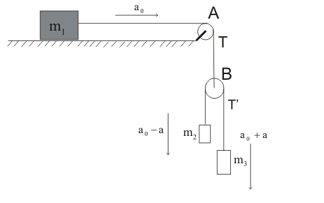
Let draw the free body diagram for each items
(a) Pulley B
(b) Block $m_1$
(c) Block $m_2$
(d) Block $m_3$
Since the pulley is light ,
We should have
$T_1 =2 T_2$
For block $m_1$
$T_1=m_1a_1$ ---1
For block $m_2$
$m_2g -T_2=m_2(a_1 - a_2)$
Or
$m_2g - \frac {T_1}{2}=m_2(a_1 - a_2)$ --2
Force block $m_3$
$m_3g -T_2=m_3(a_1 +a_2)$
or
$m_3g - \frac {T_1}{2}=m_3(a_1 +a_2)$ -3
Solving equation 1,2 and 3 we get
$a_1=\frac{g}{1+\frac{m_1}{4}(\frac{1}{m_2}+\frac{1}{m_3})}$
$T_1=\frac{m_1g}{1+\frac{m_1}{4}(\frac{1}{m_2}+\frac{1}{m_3})}$

(a) The limiting friction is given by
$=\mu N$
Where N is the normal contact force between the block
Now $N=m_1g=3 \times 10=30$N
So Limiting friction($f_{max}) =.3 \times 30=9 \ N$

(b) The only force responsible for acceleration on the upper block in the friction force
So
Maximum Acceleration=Limiting Friction/m
$a_{max}=\frac {9}{3}=3 \ m/sec^2$

(c) Maximum acceleration of the upper block=$3 \ m/s^2$
So both the block will move together if the acceleration of the lower -block does not exceed $3 \ m/s^2$
So maximum force=$(m_1+m_2) a_{max} = 24 \ N$
(d) For F=20 N ,Since it is less the maximum Force
So both the both the block will move together
$\text{Acceleration}=\frac {20}{8}=2.5 \ m/sec^2$
Friction force acting between the block=$m_1a=3 \times 2.5=7.5 \ N$

(d)Normal contact force between the block
$N=m_1g=3 \times 10=30 \ N$

(e) Normal Contact force between the larger block and surface
$N=(m_1+m_2)g=80 \ N$

(f) For F =41 N,since it is greater then maximum force,both the block will have different acceleration
For upper block
$F_{max}=m_1a_1$
Or $9=3a_1$ or $a_1=3 \ m/s^2$
For larger block
$F- F_{max}=m_2a_2$
$41-9=8a_2$
Or $a_2=4 \ m/sec^2$

(h) If the force is applied on the upper block
The only force responsible for motion of the Lower block is the frictional force
So Maximum acceleration of the lower block= Limiting Friction/m =9/5=$1.8 \ m/sec^2$
Maximum acceleration of the lower block=$1.8 \ m/sec^2$
So both the block will move together if the acceleration of the lower -block does not exceed $1.8 \ m/sec^2$
So maximum force=$(m_1+m_2) a_{max} = 14.4 \ N$

The forces acting on the object
Weight of the body acting downward (Mg)
N pressure force exerted by the lift floor on the object in upward direction( this is the same pressure force exerted by the object on the lift floor)
(a) if the lift is stationary
$Mg - N =0$
So $N =mg$

(b) if the lift is moving upward with acceleration a
$N-Mg=Ma$
Or $N=M(a+g)$

(c) if the lift is moving downward with acceleration a
$Mg-N=Ma$
Or $N=M(g-a)$

(d) if the lift is falling freely
$N-Mg=Mg$
Or $N=0$

(e) if the lift is moving upward with constant velocity
$a=0$
so $N=Mg$

(f) if the lift is moving downward with constant velocity
$a=0$
so $N=Mg$

Let y be the length of string lying on the surface of the table at any instant during the fall.If additional length dx of the strings falls on the surface in time dt.The velocity of this part when it strikes the surface of the table is given by
$v^2=u^2 + 2gx$
Now as u=0
So $v=\sqrt{2gx}$

Now the total force on the surface of the table
=rate of change of Momentum of the length dx+ weight of the length of the string lying on the surface of the table
$F=\frac{d}{dt}(mdxv) + mxg$
$ =mv\frac{dx}{dt}+mxg$
$=mv^2 + mxg$
$=2mgx + mxg$
$=3mgx$
$ =3Mg$

As M=mx

Let $T_1$ be the tension in the left cord
$T_2$ be the tension in the right cord.
The system will move from left to right as $M_3$ has the larger mass
Let a be the acceleration of the system
For Block A
$T_1 20=2a$ ----(1)
For block B
$T_2 f T_1 = 3a$
Now Frictional force $f= =.2 \times 3 \times 10=6 \ N$
As the body is in vertical equilibrium so N=mg
So
$T_2 6 T_1 = 3a$ --(2)
For block 3
$60 T_2=6a$ ---(3)
Adding 1 ,2 and 3 we get
$60 -6-20=11a$
Or $a=\frac {34}{11}=3.09 \ m/s^2$
Now from equation 1
$T_1=20+ 2 \times 3.09=26.18 \ N $
From equation 3,we get
$T_2=60-6 \times 3.09=41.46 \ m/s^2$

(a) From the frame of reference of Box Car,A pseudo force has to be introduced to apply the Newton second law of motion
So Pesudo force=-8i N
So from Newton second law,
Acceleration would be
-8i=2a
Or a = (-4) i
Now we know from kinematics
v=u+at
So
v=10i -4t i
So
$\frac{dx}{dt}=10-4t$
Or
x=10t-2t² +c
At t=0 x=c
Time at which it will return to its original place
c=10t-2t² +c
or t=5 sec

(b) From the frame of reference of Box Car,A pseudo force has to be introduced to apply the Newton second law of motion
So Pesudo force=-8i N
Also since the object is moving,a frictional force will also act to prevent the relative motion .
Friction force=$\mu mg=.3 \times 2 \times 10=6 \N$
So from Newton law
-8i – 6i=2a
Or a=-7i

The object will move till the velocity becomes zero.At that point .Static friction will come into picture .Since the value of static friction=.5*2*10=10N is greater then pseudo force.The object will stay there only
Now we know from kinematics
v=u+at
So
v=10i -7t i
So
$\frac{dx}{dt}=10-7t$
Or
x=10t-3.5t² +c

Let’s first check out the force acting on the bead
The Reaction force of the rod on the bead which is at right angle to the rod. There is no other force acting. Let the reaction force is N. Let w be the acceleration of the bead wrt to ground, then
N=Mw
The relative acceleration of the bead with respect to rod will be given by
w_r = w – a
The vectors are shown below in figure
From the triangle ,it is clear that
w_r=acosα
w=asinα
So N=Masinα
Now the time period which the bead moves along the rod
$s=\frac{1}{2}w_rt^2$
Or $t=\sqrt{\frac{2s}{acos{\alpha}}}$

As long as the object A touched the body B, the velocity of the body B is equal to the horizontal components of the velocity of the load A.
Similarly acceleration of the body B is equal to the horizontal components of the acceleration of the load A.

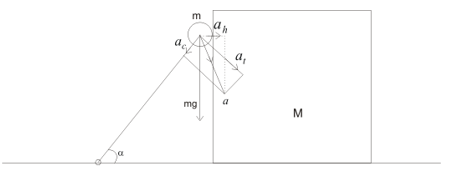
Let a be the total acceleration of the load A. Now Since the load will be moving along circular path, this can be written as
$\mathbf{a}=\mathbf{a_t}+ \mathbf{a_c}$
Where $\mathbf{a_t}$ = Tangential acceleration of the load
$\mathbf{a_c}$=centripetal acceleration of the load
Now $a_c=\frac {v^2}{L}$ where v is the velocity of the load and it is directed towards center
The horizontal components of the acceleration can be written as
$ a_h=a_tsin{\alpha}-\frac{v^2}{L}cos{\alpha}$
Now body B also has the same acceleration, we can write
$N=Ma_h$
$N=Ma_tsin{\alpha}-M\frac{v^2}{L}cos{\alpha}$
At the moment of separation N=0
So
$a_t sin{\alpha}=\frac {v^2 cos {\alpha}}{L}$ ----(1)
Now the tangential acceleration at the time of separation will be because of force of gravity
So
$a_t=gcos{\alpha}$ ---(2)
Solving (1) and (2)
We get
$v=\sqrt{gLsin{\alpha}}$
or
$\mathbf{v}=(sin{\alpha}\sqrt{gLsin{\alpha}})\mathbf{i}-(cos{\alpha}\sqrt{gLsin{\alpha}})\mathbf{j}$
And velocity of the body B
$u=vsin \alpha$
or
$u=sin{\alpha}\sqrt{gLsin{\alpha}}$
Or
$\mathbf{u}=(sin{\alpha}\sqrt{gLsin{\alpha}})\mathbf{i}$
Centripetal acceleration of the body A =$\frac {v^2}{L}= g sin{\alpha}$
Now According to law of conservation of energy, we have
$mgL=mgLsin{\alpha}+\frac{1}{2}mv^2+\frac{1}{2}Mu^2$
$mgL=mgLsin{\alpha}+\frac{1}{2}mgLsin{\alpha}+\frac{1}{2}MgL{sin}^3{\alpha}$
Or
$\frac{M}{m}=\frac{2-3sin{\alpha}}{{sin}^3{\alpha}}$
For $\alpha=30$
M/m=4
Now velocities of A and B
$\mathbf{v}=(sin{\alpha}\sqrt{gLsin{\alpha}})\mathbf{i}-(cos{\alpha}\sqrt{gLsin{\alpha}})\mathbf{j}$
$\mathbf{v}=\sqrt{\frac{gL}{8}}\mathbf{i}- \frac{3gL}{8}\mathbf{j}$
$\mathbf{u}=\sqrt{\frac{gL}{8}}\mathbf{i}$