Problems on similar triangles for class 10

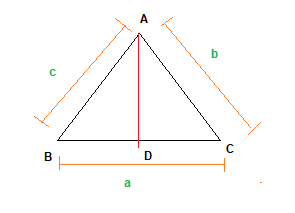
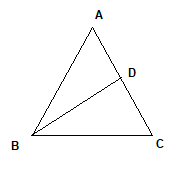
From Angle Bisector theorem
$\frac {AC}{AB} = \frac {CD}{BD}$
$\frac {b}{c}=\frac {CD}{BD}$
$\frac {b}{c} + 1 =\frac {CD}{BD} +1$
$\frac {b+c}{c}= \frac {CD+BD}{BD}$
$\frac {b+c}{c}= \frac {BC}{BD}$
$\frac {b+c}{c}= \frac {a}{BD}$
$BD= \frac {ac}{b+c}$

Now,
$CD = BC -BD$
$CD= a - \frac {ac}{b+c}$
$DC = \frac {ab}{b+c}$

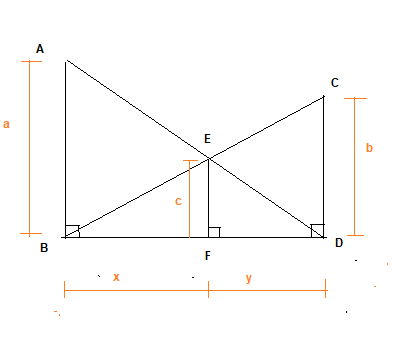
Let FB=x and FD=y
Now in $\Delta ABD$ and $\Delta EFD$
$\angle ABD= \angle EFD$
$\angle ADB= \angle EDF$ (common angle)
By SS criteria,
$\Delta ABD \sim \Delta EFD$
$\frac {AB}{EF} = \frac {BD}{FD}$
$\frac {a}{c} = \frac {x+y}{y}$
$\frac {a}{c} -1 = \frac {x+y}{y} -1$
$\frac {a-c}{c}= \frac {x}{y}$ -(1)

Now in $\Delta CDB$ and $\Delta EFB$

$\angle CDB= \angle EFB$
$\angle CBD= \angle EBF$ (common angle)
By SS criterio,
$\Delta CDB \sim \Delta EFB$
$\frac {CD}{EF} = \frac {BD}{FB}$
$\frac {b}{c} = \frac {x+y}{x}$
$\frac {b-c}{c} = \frac {y}{x}$
or $\frac {x}{y} = \frac {c}{b-c}$ -(2)
From (1) and (2)
$\frac {a-c}{c}=\frac {c}{b-c}$
$(a-c)(b-c)=c^2$
$ab -ac -bc + c^2=c^2$
$c= \frac {ab}{a+b}$

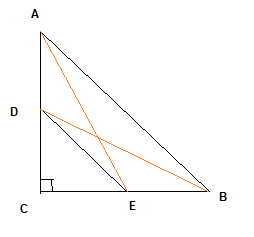
This can be easily solved using Pythagorus theorem
In Right angle triangle ACE,By Pythagoras Theorem
$AC^2+ CE^2�= AE^2$� --(1) � �
In Right angle triangle DBC,By Pythagoras Theorem
$DC^2+ BC^2 =�BD^2$�-(2) �
In Right angle triangle ABC,By Pythagoras Theorem
$AC^2�+ BC^2�= AB^2$ ---(3) ���

In Right angle triangle DEC,By Pythagoras Theorem
$DC^2�+ CE^2�= DE^2$�---(4) �

? Adding (1) and (2) we get,
$AE^2�+ BD^2�= AC^2�+ CE^2+ DC^2+ BC^2$
$= (AC^2�+ BC^2) + (CE^2+ DC^2)$

Now from (3) and (4)
$AE^2 + BD^2 = AB^2 + DE^2$

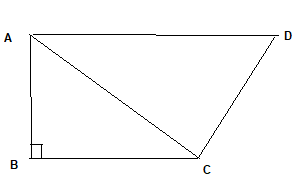
It is given $\angle B = 90$
In right angle triangle ABC
$AC^2 = AB^2 + BC^2$ -(1)
Now it is given
$AD^2= AB^2 + BC^2 + CD^2$
From (1)
$AD^2 = AC^2 + CD^2$
By converse of Pythagoras theorem
$\angle ACD = 90$

Now given
$BC^2 =AC \times CD$
$ \frac {BC}{AC} = \frac {CD}{BC}$

In $\Delta ABC$ and $\Delta BDC$
$ \frac {BC}{AC} = \frac {CD}{BC}$
$\angle ACB = \angle BCD$
Hence
$\Delta ABC \sim \Delta BDC$
By CPCT
$\frac {BD}{BC} = \frac {AB}{AC}$
Now AB =AC
$\frac {BD}{BC}=1$
BD=BC

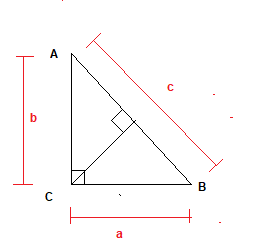
Area of the Triangle ABC
$=\frac {1}{2} \times base \times height$
Now
Area of the Triangle ABC=$\frac {1}{2} \times a \times b= \frac {ab}{2}$
Now it can be also calculated as
Area of the Triangle ABC=$\frac {1}{2} \times c \times p= \frac {pc}{2}$
Since area is equal
$\frac {ab}{2}=\frac {pc}{2}$
$cp =ab$ -(1)

Now in right angle triangle ABC
$AC^2 = AB^2 + BC^2$
$c^2 = a^2 + b^2$
From (1)
$( \frac {ab}{p})^2 = a^2 + b^2$
$\frac {a^2b^2}{p^2} = a^2 + b^2$
Dividing by $a^2b^2$
$ \frac {1}{p^2}= \frac {1}{a^2}+ \frac {1}{b^2}$

This question is exactly similar to Question 2. Please check the solution

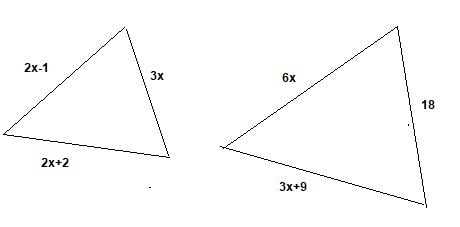
Given
$ \Delta ABC \sim \Delta DEF$
Therefore,
$\frac {AB}{DE} =\frac {BC}{EF}=\frac {CA}{FD}$
So,
$\frac {2x-1}{18}=\frac {2x+2}{3x+9}= \frac {3x}{6x}$
$\frac {2x-1}{18}=\frac {2x+2}{3x+9}$
or
$x = 5$
Therefore,
AB = 2 * 5 �1= 9, BC = 2 * 5 + 2 = 12,
CA = 3 * 5 = 15, DE = 18, EF = 3* 5 + 9 = 24 and FD = 6 * 5 = 30
Hence, AB = 9 cm, BC = 12 cm, CA = 15 cm
DE = 18 cm, EF = 24 cm and FD = 30 cm

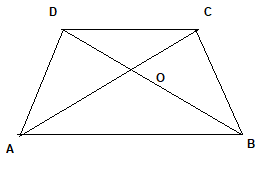
In $\Delta AOB$ and $\Delta COD$, we have
$\angle AOB= \angle COD$ ( Vertically Opposite angles)
$\angle OCD= \angle OAB$ ( Alternate angles)
$\angle ODC=\angle OBA$ ( Alternate angles)
by AAA similarity
$\Delta AOB \sim \Delta COD$
Now Area of Similar Triangle is given by
$\frac {Area AOB}{Area COD} = \frac {AB^2}{CD^2}$
Now AB= 2CD
Hence
$\frac {Area AOB}{Area COD} = \frac {4}{1}$

a. False
b. True
c. False
d. True

(a)ratio of the corresponding sides.
(b) sides
(c) $\Delta CAB$
(d) equal