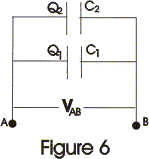
Question 1
A network of five capacitors of C is connected to a 100 V supply, as shown in below figure. Determine
(a) the equivalent capacitance of the network
(b) the charge on each capacitor.
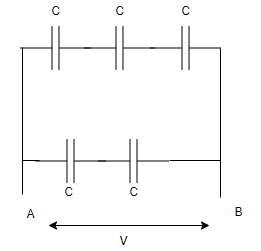 Solution
Solution
In the given network , the top three Capacitance is in series, So equivalent capacitance of top part
$\frac {1}{C_1} = \frac {1}{C}+\frac {1}{C}+ \frac {1}{C}$
$C_1 = \frac {C}{3}$
Similarly, the lower two Capacitance is in series, So equivalent capacitance of lower part
$\frac {1}{C_2} = \frac {1}{C}+\frac {1}{C}$
$C_2 = \frac {C}{2}$
Now both $C_1$ and $C_2$ are in parallel, so equivalent Capacitance of the Network
$C_{eq} = C_1 + C_2 = \frac {C}{3} + \frac {C}{2}= \frac {5C}{3}$
Now Charge on top part will be
$Q_1 = C_1 V = \frac {CV}{3}$
Now Charge on lower part will be
$Q_2 = C_2 V = \frac {CV}{2}$
Question 2
Find the equivalent Capacitance between point P and Q
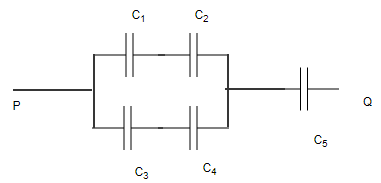
Here $C_1=2 \ \mu F$,$C_2=4 \ \mu F$,$C_3=8 \ \mu F$,$C_4=10 \ \mu F$,$C_5=12 \ \mu F$
Solution
In the given network ,$C_1$ and $C_2$ are series, so equivalent capacitance C' for that will be
$\frac {1}{C'}=\frac {1}{C_1}+ \frac {1}{C_2}$
or
$C'=4/3 \ \mu F$
In the given network ,$C_1$ and $C_2$ are series, so equivalent capacitance C'' for that will be
$\frac {1}{C''}=\frac {1}{C_3}+ \frac {1}{C_4}$
or
$C''=40/9 \ \mu F$
Now C' and C'' are in parallel,so it can be replaced with the equivalent capacitance $C_p$
$C_p=C'+ C''=52/9 \mu F$
Now $C_p$ and $C_5$ are in series, so net equivalent capacitance will be
$C_{eq} = \frac { C_p C_5}{C_p + C_5} = \frac {52/9 \times 12}{52/9 + 12} =3.9 \mu F$