

Following the notes, you will find questions and answers that can benefit you in class 12 Board exams and other competitive exams. We will also provide assertion reason-type questions, as they are frequently asked in exams.
Current density is an important concept in various areas of physics, such as in the study of electrical circuits, semiconductors etc.
Current density is a vector quantity that describes the amount of electric current flowing through a unit cross-sectional area perpendicular to the flow of the current within a conducting material.
Current density is a measure of how much electric current is flowing through a particular area in a given amount of time. For better idea, imagine a wire carrying an electric current. The current density would tell you how much charge is passing through a cross-sectional area of that wire per unit time. The higher the current density, the more charge is flowing through that area.
It gives insight into the distribution and concentration of electric current at different points in the conductor.
When electric current flows through a conductor, such as a copper wire, it is not always uniformly distributed across the entire cross-section of the conductor. Instead, the current can be more concentrated in some areas and less concentrated in others. The current density tells us about this distribution of electric current within the conductor.
In simpler terms, imagine a highway with multiple lanes. The cars on the highway represent the flow of electric current in a conductor. In some lanes, the cars might be more densely packed together, while other lanes might have fewer cars. The current density provides us with a way to quantify the distribution and concentration of cars (electric current) in each lane (point in the conductor).
Because it's a vector, we usually represent it with the symbol "J" (a bold J). It is also written as vec J in vector notation or handwritten form.
It's a vector quantity, meaning it has both magnitude and direction. The direction of current density is the same as the direction of current.
This means that if the charges moving in a conductor are positive, then the current density will be in the same direction as the motion of these charges.
However, if the charges are negative, then the current density will be in the opposite direction to the motion of these charges.
To get the formula for current density let us consider an observation point $P$ inside the conductor. Now draw an infinitesimally small area $\Delta A$ around the observation point.
Let $\Delta I$ be the current through the area $\Delta A$. The current density at this point $P$ is defined as
$\vec J=\lim_{\Delta A \rightarrow 0}\frac{\Delta I}{\Delta A}\hat n=\frac{dI}{dA}\hat n$
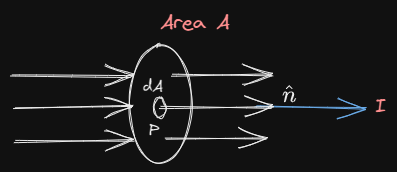
If the electric current is uniformly distributed over an area $A$, then current density would be constant at all points. In this case
$J=\frac{I}{A}$
When current is not perpendicular to the area
If normal to the area makes an angle \theta with the direction of current as shown below in the figure
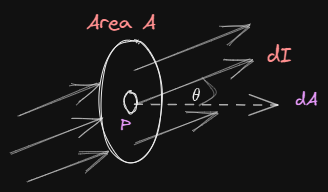
then in this case component of dA normal to the direction of current flow will be, $$dA_n=dA\cos\theta$$ therefore, current density $$J=\frac{dI}{dA\cos\theta}$$ $$\Rightarrow \quad dI=JdA\cos\theta or, dI=\vec J\cdot d\vec A$$ or, $$I=\int_{A}\vec J\cdot d\vec A \tag{1}$$ So, the current $I$ through a particular surfece A in a conductor is the flux of \vec J through the surface and is given by surface integral in eqiation (1).
SI unit of current is Ampere per squate meter $(Am^{-2})$
Dimension dormula of electric current density is $[AL^{-2}]$

Definition: The amount of electric charge passing through a conductor per unit of time.
Macroscopic property: Describes the large-scale behavior or phenomenon.
Symbol: I
Unit: Ampere (A)
Formula: I = ΔQ/Δt (where ΔQ is the change in electric charge, and Δt is the change in time)
Definition: The amount of electric current passing through a unit cross-sectional area perpendicular to the flow of the current.
Microscopic property: Describes the small-scale behavior of electric charge distribution within a conducting material.
Symbol: J
Unit: Amperes per square meter (A/m²)
Formula: J = I/A (where I is the electric current, and A is the cross-sectional area)

Question 1. A copper wire has a cross-sectional area of 2 mm² and carries a current of 5 A. What is the current density in the wire?
Answer: $J = \frac{I}{A} = \frac{5 A}{(2 \times 10^{-6} m^2)} = 2.5 \times 10^6 A/m^2$
Question 2. A silver wire has a current density of 3 A/mm². If the wire has a cross-sectional area of 4 mm², what is the current flowing through the wire?
Answer: $I = J \times A = 3 A/mm^2 \times (4 \times 10^{-6} m^2)$
$ = 1.2 \times 10^{-5} A$
Question 3. An electron beam has an aperture of $1.0\text{ mm}^2$. A total of $6\times 10^{16}$ electrons flow through any perpendicular cross-section per second. Calculate
(i) the current (ii) the current density in the electron beam.
Answer: (i) $I=\frac{q}{t}=\frac{ne}{t}$
$=\frac{6\times 10^{16} \times 1.6 \times 10^{-19}}{1} =9.6\times 10^{-3}A$
(ii) Current density $J=\frac{I}{A}=\frac{9.6\times 10^{-3}}{1.0\times 10^{-6}} =9.6 \times 10^{3}Am^{-2}$
For following questions two statements are given one labelled as Assertion (A) and the other labelled as Reason (R). Select the correct answer to these questions from the codes (a), (b), (c) and (d) as given below.
(a) Both A and R are true and R is the correct explanation of A
(b) Both A and R are true but R is NOT the correct explanation of A
(c) A is true but R is false
(d) A is false and R is also true
Question 1.
Assertion (A): The current density in a conductor is directly proportional to the electric field applied across it.
Reason (R): Ohm's law states that the current density in a conductor is equal to the product of the conductivity and the electric field.
Answer: Option (a)
Explanation: The assertion is true as the current density (J) in a conductor is directly proportional to the electric field (E). The reason is also true and explains the assertion, as Ohm's law relates the current density, conductivity (σ), and electric field through the equation J = σE.
Question 2.
Assertion (A): In a uniform conductor, the current density is constant throughout the conductor.
Reason (R): In a uniform conductor, the electric field is uniform and the conductivity remains constant.
Answer: Option (b)
Explanation: Both the assertion and reason are true. In a uniform conductor, the current density remains constant because the electric field and the conductivity are constant. However, the reason is not a direct explanation for the assertion, as it does not explicitly mention the relationship between current density, electric field, and conductivity.
Question 3.
Assertion (A): The drift velocity of electrons in a conductor is independent of the electric field.
Reason (R): The drift velocity of electrons is proportional to the electric field applied across a conductor.Answer: Option (d)
Explanation: The assertion is false because the drift velocity of electrons in a conductor depends on the electric field. The reason is true, as the drift velocity of electrons is indeed proportional to the electric field applied across the conductor.
Question 4.
Assertion (A): Current density is a scalar quantity.
Reason (R): Current density has both magnitude and direction.Answer: Option (b)
Explanation: The assertion is false because current density is a vector quantity, as it has both magnitude and direction. The reason is true, as it correctly states the properties of current density. However, the reason does not directly explain the assertion, as the assertion itself is incorrect.
Question 5.
Assertion (A): The current density in a conductor is independent of the charge density.
Reason (R): The current density is determined by the drift velocity of charge carriers and the number of charge carriers per unit volume.Answer: Option (d)
Explanation: The assertion is false because the current density $(J)$ in a conductor is related to the charge density. The reason is true, as the current density is determined by the drift velocity $(v_d)$ of charge carriers and the number of charge carriers $(n)$ per unit volume, multiplied by the charge $(q)$ of the charge carriers: $J = nqv_d$. The reason does not directly explain the assertion because the assertion is incorrect.
Question 1. Which of the following is the correct formula for current density?
a) J = I/A
b) J = A/I
c) J = I \times A
d) J = A - I
Answer: a) J = I/A
Question 2. Which of the following materials would have the highest current density?
a) Copper
b) Aluminum
c) Silver
d) Iron
Answer: c) Silver
Question 3. What is the SI unit of current density?
a) A/m
b) A/m²
c) A/m³
d) A/m⁴
Answer: b) A/m²
Question 4. A wire has a current density of 4 A/mm². If the wire has a cross-sectional area of 3 mm², what is the current flowing through the wire?
a) 12 A
b) 0.75 A
c) 1.33 A
d) 0.25 A
Answer: a) 12 A
Question 5. Which of the following statements is true about current density? a) It is a measure of the resistance of a material. b) It is a measure of the amount of electric charge flowing through a conductor. c) It is a measure of the amount of electric current flowing through a unit area of a conductor. d) It is a measure of the voltage drop across a conductor.
Answer: c) It is a measure of the amount of electric current flowing through a unit area of a conductor.