

In this comprehensive guide, you'll gain a deep understanding of the concept of drift velocity, Relationship Between Drift Velocity and Electric Current and solved questions and answers for these exams. This concept is crucial for Class 12 Physics and competitive exams like NEET and JEE. It includes detailed explanations, formulae, units, dimensions, derivation and solved examples tailored to your exam preparation needs.
Metallic conductors are characterized by a large number of free electrons, known as conduction electrons. These electrons are derived from the valence electrons of atoms. At room temperature, conduction electrons move randomly inside the conductor, much like gas molecules.
During their motion, conduction electrons frequently collide with ions, which are the positively charged atoms left after valence electrons have moved away. The direction of electron motion changes after each collision, causing the electrons to follow a zig-zag path.
In a conductor, the large number of electrons move randomly. If we imagine an area within the conductor, the number of electrons crossing this area from left to right is nearly equal to the number crossing from right to left in a given time interval.
This balanced movement of electrons means that there's no net flow of electric current through that area without an external electric field. The drift of electrons and hence the flow of electric current begins only when an electric field is applied.
When a potential difference is applied across a conductor, an electric field is established within it. This field exerts a force on the conduction electrons, causing them to accelerate in the direction opposite to the field. This acceleration, however, is short-lived as the electrons continually collide with positive ions, losing their gained kinetic energy.
Applying a Potential Difference
Let's start by applying a potential difference (also known as voltage) across a conductor, such as a wire, using a battery. This creates an electric field within the conductor.
The Effect of the Electric Field on Conduction Electrons
When an electric field is established inside the conductor, the conduction electrons (which are free to move) experience a force. This force acts in the direction opposite to the electric field, which causes the electrons to accelerate.
Electrons Drifting and Collisions
As a result of this acceleration, the electrons start to drift or move slowly along the length of the conductor. They move towards the end of the conductor that is attached to the positive terminal of the battery (or the end at a higher potential).
However, the acceleration and the increase in velocity of the electrons don't last long. This is because the conductor is full of positive ions, and the accelerated electrons frequently collide with these ions.
The Effect of Collisions
Every time a collision occurs, the electron loses its kinetic energy and its direction changes randomly. After each collision, the process repeats: the electron gets accelerated again by the electric field, gains some velocity, and then loses that gained kinetic energy in another collision.
This cycle of gaining and losing velocity continues until the electrons reach the positive end of the conductor. The net effect of this process is that, under the influence of the electric field, the electrons 'drift' through the conductor, which is the basis of electric current.
Understanding Drift Velocity and the Impact of Electric Field on Free Electrons
In a conductor, under the influence of an electric field, free electrons behave in a specific way. They have a random motion due to the thermal energy at room temperature, but they also gain a small additional velocity that causes them to drift towards the positive end of the conductor.
To understand this drift velocity, let's define some variables. Let $\tau$ represent the average time between two successive collisions of an electron, and let $E$ denote the strength of the applied electric field.
Given that the charge on an electron is $e$, the force on the electron due to the electric field is given by the equation:
$$F = -eE $$
If $m$ is the mass of the electron, the acceleration produced by this force is given by:
$a = -\frac{eE}{m}$
As the electron is accelerated over the average time interval $\tau$, it acquires an additional velocity, often referred to as the drift velocity ($v_d$). We can express this mathematically as:
$v_d = a\tau$
Substituting the value of $a$ into this equation, we get:
$v_d = \frac{eE}{m}\tau$
This drift velocity is a small additional velocity imposed on the random thermal motion of the electrons due to the applied electric field. It represents the average velocity with which free electrons drift towards the positive end of the conductor when influenced by an external electric field. This drift of electrons is the fundamental mechanism behind the flow of electric current.
Drift velocity definition
Drift velocity is defined as the velocity with which free electrons get drifted towards the positive end of the conductor under the influence of an externally applied electric field.
We start with a conducting wire. This wire is of length $L$ and has a uniform cross-sectional area $A$. Inside this wire, an electric field is present.
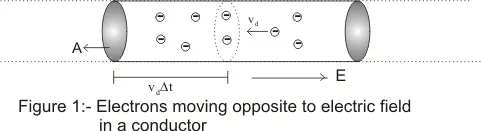
Electrons in the Conductor
In this wire, we have a number of free electrons per unit volume. We denote this quantity as $n$. These electrons are moving with a certain average velocity, known as the drift velocity, which we denote as $v_d$.
Observing Electron Movement: The Role of Time
Now, let's observe what happens in a small time interval $\Delta t$. In this time, each electron moves forward by a distance equal to the drift velocity times the time interval, or $v_d\Delta t$.
Visualizing Electron Movement: The Volume Covered
Imagine a slice of the wire where the electrons have moved. The volume of this slice is the cross-sectional area $A$ times the distance the electrons have moved, or $A v_d\Delta t$.
Counting Electrons: How Many Have Moved?
The number of free electrons within this slice of wire is the volume of the slice times the number of electrons per unit volume, or
Number of electrons in wire of length $L$ and cross-sectional area $A$= $n A v_d\Delta t$.
Calculating Charge Transfer: How Much Charge Has Moved?
All these electrons within the slice cross the cross-sectional area $A$ in our time interval $\Delta t$.
So, the total charge $\Delta Q$ that moves across this area in this time is the number of electrons times the elementary charge $e$ (the charge of a single electron), or
$\Delta Q = neA v_d\Delta t$
Defining Current: Charge Over Time
The electric current $I$ is defined as the charge $\Delta Q$ that crosses a given area per unit of time $\Delta t$. Therefore, we can write
$I = \frac{\Delta Q}{\Delta t} = neA v_d$.
This equation shows the relationship between electric current and drift velocity.
Considering Positive Charge Carriers: A Change in Direction
If we consider positive charge carriers instead of electrons, the situation changes a bit. The force from the electric field on these positive charge carriers would be in the same direction as the electric field. Therefore, their drift velocity would also align with the direction of the electric field, opposite to what happens with negative charge carriers like electrons.
Current Density: Current per Unit Area
We can also define a quantity called the current density $\vec j$, which is the electric current $I$ divided by the cross-sectional area $A$. (see also Current Density definition)
In terms of drift velocity, we can express this as
$\vec j = \frac{I}{A} = ne \vec{v_d}$.
The above equation is valid for both positive and negative values of $q$.

Question 1. How is the drift velocity in a conductor affected with the rise in temperature? (CBSE Delhi Set-III 2019)
Answer. As the temperature of a conductor increases, the speed of electrons (drift velocity) generally decreases because the atoms in the conductor vibrate more, causing more collisions with the electrons and slowing them down.
Question 2. How does the drift velocity in a conductor change with increase of flowing current ?
Answer. The drift velocity ($v_d$) in a conductor is directly proportional to the current (I) flowing through it. This is expressed by the formula:
$v_d = I / (nAe)$
where:
From this equation, you can see that if the current $(I)$ increases, the drift velocity $(v_d)$ will also increase, assuming the number of free charge carriers $(n)$, the cross-sectional area of the conductor $(A)$, and the charge of an electron $(e)$ remain constant.
So, if you increase the current flowing through a conductor, the drift velocity of the electrons will also increase, leading to a higher rate of electron flow. (If it is a one mark question only write this sentence)
Question 3. What happens to the drift velocity of electron and to the resistance $R$, if length of the conductor is dubled keeping the potential difference unchanged? (2002)
Answer.
Effect of length on drift velocity
Drift velocity in terms of relaxation time:
$\vec{v_d}=\frac{-e\vec E}{m}\tau$
For uniform electric field,
$vd=\frac{cV\tau}{lm}\text{ (in magnitude)}$
So,
$v_{d}\propto\frac{1}{l}$
So, if length is doubled, drift velocity is halved.
Effect on resistance
We know that resistance $R\propto l$. So, if length is doubled resistance is also doubled.
Question 4. A conductor of length $l$ is connected to a DC source of EMF $\mathcal{E}$. The length of the conductor is tripled by stretching it keeping $\mathcal{E}$ constant. How would drift velocity be affected. (2015)
Solution.
Drift velocity in terms of relaxation time:
$\vec{v_d}=\frac{-e\vec E}{m}\tau$
For uniform electric field,
$v_d=\frac{cV\tau}{lm}\text{ (in magnitude)}$
So,
$v_{d}\propto\frac{1}{l}$
So, if length is tripled, drift velocity becomes one thired (1/3)rd.
Question 5. The number density of free electrons in a copper conductor estimated is $8.5 \times 10^{28} m^{−3}$. How long does an electron take to drift from one end of a wire 3.0 m long to its other end? The area of cross-section of the wire is $2.0 \times 10^{−6} m^2$ and it is carrying a current of $3.0 A$. (NCERT)
Solution.
Number density of free electrons in a copper conductor, $n = 8.5 \times 10^{28} m^{−3}$
Length of the copper wire, $l = 3.0 m$
Area of cross-section of the wire,$A = 2.0 \times 10^{−6} m^2$
Current carried by the wire, $I = 3.0 A$,
which in terms of drift velocity is given by the relation,
$$I=neAv_d$$
Where,
e = Electric charge $= 1.6 \times 10^{−19} C$
$V_d =$ Drift velocity $=\frac{\text{Length of the wire }(l)}{\text{time taken}}$
$I=neA(\frac{l}{t})$
$t=\frac{neAl}{I}$
Now putting in all the known values we get,
$t=\frac{3\times 8.5 \times 10^{28} \times 2.0 \times 10^{−6} \times 1.6 \times 10^{−19}}{3.0}$
Therefore, the time taken by an electron to drift from one end of the wire to the other is $2.7 \times 10^4 s$.
For following questions two statements are given one labelled as Assertion (A) and the other labelled as Reason (R). Select the correct answer to these questions from the codes (a), (b), (c) and (d) as given below.
(a) Both A and R are true and R is the correct explanation of A
(b) Both A and R are true but R is NOT the correct explanation of A
(c) A is true but R is false
(d) A is false and R is true
Question 1: Assertion (A): The drift velocity of electrons in a conductor is proportional to the electric field applied across the conductor. Reason (R): The drift velocity is caused due to the force exerted by the electric field on the free electrons in the conductor.
Answer: Option A
The assertion and the reason are true and the reason correctly explains the assertion. Drift velocity is indeed proportional to the electric field and is caused by the force exerted by the electric field on the free electrons.
Question 2: Assertion (A): The drift velocity of electrons in a conductor decreases with increasing temperature. Reason (R): With an increase in temperature, the number of free electrons in the conductor increases.
Answer: Option B
Both the assertion and the reason are true, but the reason doesn't correctly explain the assertion. Drift velocity decreases with increasing temperature due to increased thermal agitation of atoms leading to more frequent collisions, not because the number of free electrons increases.
Question 3: Assertion (A): The drift velocity is directly proportional to the square of the charge on the electron. Reason (R): The drift velocity is the average velocity gained by the charge carriers under the influence of an electric field.
Answer: Option D
The assertion is false as drift velocity is not directly proportional to the square of the charge on the electron. However, the reason is correct. The drift velocity indeed is the average velocity gained by the charge carriers due to the electric field.
Question 4: Assertion (A): Increasing the electric field across a conductor will decrease the drift velocity of the electrons. Reason (R): An increased electric field causes more frequent collisions between the electrons and the atoms in the conductor.
Answer: Option C
The assertion is false. Increasing the electric field across a conductor actually increases the drift velocity of the electrons, not decreases it. The reason is also false as an increased electric field doesn't necessarily cause more frequent collisions, but increases the speed at which electrons move between collisions.
Question 1. A steady current flow in a metallic conductor of non-uniform cross-section. The quantity/quantities remaining constant along the whole length of the conductor is/are:
a. current, electric field and drift speed
b. drift speed only
c. current and drift speed
d. curent only
Answer. Correct answer is (d)
Explaination. In a conductor of non-uniform cross-section, the current remains constant throughout the conductor due to the conservation of charge. This is based on Kirchhoff's current law, which states that the total current entering a junction or section of a circuit must equal the total current leaving it.
However, the electric field and drift speed do not remain constant. The electric field varies based on the resistance of the different parts of the conductor, which would change due to the varying cross-section. The drift speed or drift velocity, which is the average velocity of the charge carriers (usually electrons in a metal) under the influence of an electric field, will also change.
In areas of the conductor with a smaller cross-sectional area, the same current will correspond to a larger drift speed, because the charge carriers have less area to move through, so they must move faster to maintain the same current. Conversely, in areas with a larger cross-sectional area, the drift speed will be slower. So, the drift speed varies along the length of a conductor with a non-uniform cross-section.
Question 2. What is the drift velocity of electrons in a silver wire of length $2 m$, having cross-sectional area $6.14\times 10^{−6}m^2$ and carrying a current of $5A$. Given, atomic weight of silver = 108, density of silver $=9.5\times10^3kg/m^3$, charge of electron $=1.6\times 10{−9}C$, Avogadro's number $=6.023\times 10^{26}$ per kg atom?
Solution. Drift velocity formula is given by equation
$$v_d = \frac{I}{neA}$$
Given:
Length of the wire ($l$) = $2 \, \text{m}$
Cross-sectional area ($A$) = $6.14 \times 10^{-6} \, \text{m}^2$
Current ($I$) = $5 \, \text{A}$
Charge of electron ($e$) = $1.6 \times 10^{-19} \, \text{C}$
Density of silver ($\text{density}$) = $9.5 \times 10^{3} \, \text{kg/m}^3$
Avogadro's number ($N_A$) = $6.023 \times 10^{23} \, \text{atoms/mol}$
Atomic weight of silver ($\text{atomic weight}$) = $108 \, \text{g/mol} = 0.108 \, \text{kg/mol}$
first we have to calculate the number density ($n$):
The number density of electrons can be calculated using the formula:
$$n = \frac{\text{density} \times N_A}{\text{atomic weight}}$$
Substituting the given values, we have:
$n = \frac{9.5 \times 10^{3} \times 6.023 \times 10^{23}}{0.108} \approx 5.28 \times 10^{28} \, \text{electrons/m}^3$
Step 2: Calculate the drift velocity ($v_d$):
The drift velocity of electrons can be calculated using the formula:
$v_d = \frac{I}{{n \times A \times e}}$
Substituting the given values, we have: $$v_d = \frac{5}{{5.28 \times 10^{28} \times 6.14 \times 10^{-6} \times 1.6 \times 10^{-19}}} \approx 9.60 \times 10^{-5} \, \text{m/s}$$
Therefore, the drift velocity of electrons in the given silver wire is approximately $9.60 \times 10^{-5} \, \text{m/s}$.
Please note that the values used in the calculations are rounded for simplicity.