

Master Ohm's Law with our comprehensive Class 12 Physics guide covering Chapter 3: Current Electricity. This detailed tutorial explains Ohm's Law definition, statement, and mathematical derivation from drift velocity, alongside electrical resistance concepts, dimensions, and SI units. Learn current-voltage relationships in ohmic and non-ohmic devices, understand Ohm's Law limitations, and practice with solved numerical problems, assertion-reason questions, and conceptual Q&As. Perfect for CBSE Board exam preparation, NEET Physics, and JEE Main/Advanced success. Includes step-by-step problem-solving techniques, real-world applications, and exam-focused practice questions to help students excel in electrical circuit analysis and current electricity topics.
Let us now define Ohm's law
Ohm's Law establishes the relationship between the potential difference applied across the ends of a conductor and the current flowing through it.
This law was formulated by George Simon Ohm in 1826.
The statement of Ohm's law can be expressed as:
If the physical state of the conductor (e.g., temperature, mechanical strain, etc.) remains unchanged, then the current flowing through the conductor is directly proportional to the potential difference across the two ends of the conductor.
This can be mathematically represented as follows:
In these equations, '$V$' represents the potential difference, '$I$' is the current, and '$R$' is the constant of proportionality, known as the electric resistance or simply the resistance of the conductor. The value of resistance depends on the nature, dimension, and physical characteristics of the conductor.
Understanding the Relationship:
Ohm's Law allows us to understand how changes in voltage or resistance affect the current flow in a circuit. By manipulating the equation $V = I \times R$, we can calculate and predict the behaviour of electrical systems.
Practical Examples of Ohm's Law:
Importance and Applications:
Ohm's Law is crucial in electrical engineering, electronics, and telecommunications. It helps engineers design circuits, analyse their performance, and troubleshoot issues. It serves as the foundation for understanding and working with electricity.
Ohm's Law can be derived using the drift velocity relation. Let's start with the equation:
$v_d = \frac{eE}{m}\tau$
Where electric field '$E$' can be replaced with $\frac{V}{l}$ where $V$ is the potential difference across the conductor of length $l$
The equation for drift velocity then becomes:
$v_d = \frac{eV}{ml}\tau$
Also, considering the relation $I = neAvd$, by substituting the value of '$v_d$', we get:
$I = \frac{ne^2A\tau}{ml} V$
At a fixed temperature, the quantities $m$, $l$, $e$, $\tau$ and $A$ all have constant values for any given conductor.
From this, we can express the ratio $V/I$ as:
$$\frac{V}{I}=\text{a constant, } R$$ where,
$R=\frac{ml}{ne^2A\tau}$
This gives us the Ohm's Law equation again:
$V = IR$
From Ohm's Law, we derive the equation for resistance, $R$:
$R = \frac{V}{I}$
Thus, the electric resistance of a conductor is the ratio of the potential difference across the conductor's ends and the amount of current flowing through the conductor. It's essentially the obstruction offered by the conductor to the current's flow.
The SI unit of resistance is ohm (Ω), where:
$1\Omega = \frac{\text{1 Volt}}{\text{1 Ampere}}$
or
$1\,\Omega= 1VA^{-1}$
The dimension of resistance is $[ML^2T^{-3}A^{-2}]$. Let us now learn how to find it.
The dimensions of resistance ($R$) can be derived from its definition. According to Ohm's law, resistance is the ratio of voltage ($V$) to current ($I$).
So, $R = \frac{V}{I}$
The dimensions of voltage ($V$) are $[M L^2 T^{-3} A^{-1}]$ and those of current ($I$) are $[A]$.
To find the dimensions of resistance, we divide the dimensions of voltage by those of current. This gives us the dimensions of resistance:
$\frac{[M L^2 T^{-3} A^{-1}]}{[A]} = [M L^2 T^{-3} A^{-2}]$
So, the dimensional formula for resistance is $[M L^2 T^{-3} A^{-2}]$. Here, $M$ stands for Mass, $L$ for Length, $T$ for Time, and $A$ for Electric Current.
When a potential difference is applied across a conductor, an electric field is established between its two ends. This electric field exerts a force on the free electrons within the conductor, causing them to accelerate towards the positive end.
However, as these electrons move, they constantly collide with the positive ions and other atoms in the conductor. Each collision disrupts the electron's path, effectively slowing down their overall progress towards the positive end.
This opposition to the electron flow, resulting from the atomic interactions within the conductor, is what we refer to as the 'resistance' of the conductor. It's a measure of how much a conductor impedes the electric current. This resistance depends on factors like the material's properties, its temperature, and its physical dimensions (length and cross-sectional area).
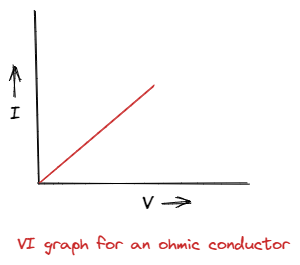
Devices obeying Ohm's Law exhibit a linear relationship between the current flowing and the applied potential difference. In other words, the current is directly proportional to the applied voltage. A graph between V and I for such devices is a straight line passing through the origin, where the slope represents the resistance.
Many electrical devices, such as vacuum tubes, semiconductor diodes, and transistors, do not obey Ohm's Law. For these non-ohmic devices, current may depend on voltage in more complex ways.
For instance, a semiconductor junction diode, used to convert alternating current to direct current and perform various logic functions, is a non-ohmic device. Its current-voltage graph exhibits a non-linear dependency, clearly deviating from Ohm's Law.
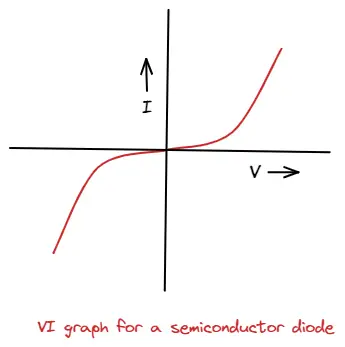
When a device doesn't obey Ohm's Law, it exhibits a non-linear voltage-current relation, and the quantity $V/I$ is no longer a constant. However, the ratio is still known as resistance, which now varies with current.
In such cases, we define a quantity $dV/dI$ known as dynamic resistance which expresses the relation between a small change in current and the resulting change in voltage. Thus for non-ohmic electrical device's resistance is not constant for different values of V and I.
Ohm's Law, while a fundamental principle in electrical circuits, does have some limitations. Here are a few key limitations to consider:
Non-Ohmic Devices: Ohm's Law is not applicable to all types of electrical devices. Some devices, like diodes, transistors, and certain types of lamps, do not follow Ohm's Law. These are called non-ohmic devices, and their current-voltage relationship is non-linear, meaning the ratio $V/I$ isn't a constant and varies with the current or voltage.
Temperature Dependence: The law assumes that the temperature remains constant, which is not always the case in practical situations. The resistance of a conductor can change with temperature. For instance, for most metals, resistance increases with an increase in temperature.
High Electric Fields: At very high electric fields, the drift velocity of electrons does not remain proportional to the electric field, which violates Ohm's law.
Superconductors: Superconductors have zero resistance when cooled to extremely low temperatures, a phenomenon that doesn't conform to Ohm's Law, which states that current is proportional to voltage (implying some resistance).
Frequency Dependence: Ohm's law may not hold for alternating currents or voltages, especially at high frequencies, where inductive and capacitive effects come into play.
In these and other similar conditions, more sophisticated models and laws of electricity are required to accurately describe the behavior of the circuit components.
For the following questions, two statements are given, one labelled as Assertion (A) and the other labelled as Reason (R). Select the correct answer to these questions from the codes (a), (b), (c) and (d) as given below. (a) Both A and R are true and R is the correct explanation of A (b) Both A and R are true but R is NOT the correct explanation of A (c) A is true but R is false (d) A is false and R is true
Question 1: Assertion: Ohm's law states that the current flowing through a conductor is directly proportional to the voltage across its ends, provided the physical conditions remain constant. Reason: The constant of proportionality in Ohm's law is known as resistance and depends on the nature and physical dimensions of the conductor. Answer: Correct Option: a Explanation: Both the assertion and reason are correct, and the reason is the correct explanation of the assertion. Ohm's law does state the direct proportionality of current and voltage, and resistance is indeed the constant of proportionality.
Question 2:
Assertion: The resistance of a conductor always remains constant regardless of the applied voltage or current.
Reason: The resistance of a conductor is determined by factors such as its material, length, cross-sectional area, and temperature.
Answer: Correct Option: b
Explanation: Although the reason is correct, the assertion is false. Resistance does not always remain constant. It can change due to factors like temperature and in the case of non-ohmic devices.
Question 3:
Assertion: Ohm's law is universally applicable to all electronic components and devices.
Reason: Some electronic devices, like diodes and transistors, do not obey Ohm's law and are referred to as non-ohmic devices.
Answer: Correct Option: d
Explanation: The assertion is false because Ohm's law is not universally applicable, especially to non-ohmic devices. However, the reason is correct and explains that certain devices like diodes and transistors are non-ohmic.
Question 4:
Assertion: Superconductors obey Ohm's law at extremely low temperatures.
Reason: Superconductors have zero resistance when cooled to extremely low temperatures.
Answer: Correct Option: b
Explanation: Both statements are true, but the reason is not the correct explanation for the assertion. Superconductors do have zero resistance at low temperatures, but this doesn't make them obey Ohm's law. Instead, it's a distinct property that makes them an exception to Ohm's law.
Question 5:
Assertion: Ohm's law is derived from the relationship between drift velocity and electric field.
Reason: The current flowing through a conductor is inversely proportional to the voltage across its ends.
Answer: Correct Option: c
Explanation: The assertion is true, as Ohm's law can indeed be derived from the relationship between drift velocity and electric field. However, the reason is false; according to Ohm's law, the current is directly, not inversely, proportional to the voltage.
Problem 1: An electric heater is designed to work on a 240 V power supply. If the heater draws a current of 8 A, what is the resistance of the heater?
Solution: Applying Ohm's law (V = I * R), where V = Voltage = 240 V I = Current = 8 A
We need to find the Resistance (R).
Rearranging the formula for R, we get R = V / I.
Substituting the values, R = 240 V / 8 A = 30 Ω.
So, the resistance of the heater is 30 Ω.
Problem 2: A circuit is formed with a 9 V battery and a resistor. The current flowing through the circuit is 1.5 A. What is the resistance of the resistor in the circuit?
Solution: Applying Ohm's law (V = I * R), where V = Voltage = 9 V I = Current = 1.5 A
We need to find the Resistance (R).
Rearranging the formula for R, we get R = V / I.
Substituting the values, R = 9 V / 1.5 A = 6 Ω.
So, the resistance of the resistor is 6 Ω.
Problem 3: An electronic device operates at a voltage of 12 V and has a resistance of 3 Ω. What is the current flowing through the device?
Solution: Applying Ohm's law (V = I * R), where V = Voltage = 12 V R = Resistance = 3 Ω
We need to find the Current (I).
Rearranging the formula for I, we get I = V / R.
Substituting the values, I = 12 V / 3 Ω = 4 A.
So, the current flowing through the device is 4 A.
Question 1: Can the resistance of a conductor be changed by altering the length or cross-sectional area of the conductor?
Answer: Yes, the resistance of a conductor can be changed by altering its physical properties. According to Ohm's law, resistance is directly proportional to the length of the conductor and inversely proportional to its cross-sectional area.
Question 2: Will the current flowing through a conductor change if the temperature of the conductor is increased, assuming the voltage remains the same?
Answer: Yes, the current flowing through a conductor will change if the temperature of the conductor is increased. The resistance of most materials changes with temperature. As temperature increases, the resistance of the conductor typically increases, resulting in a decrease in current according to Ohm's law, assuming the voltage remains the same.
Question 3: Does the resistance of a conductor depend on the material from which it is made?
Answer: Yes, the resistance of a conductor does depend on the material from which it is made. Different materials have different resistivities, which is a measure of how much they resist the flow of electricity. This is why certain materials are used for specific applications based on their resistivity.
Question 4: Would changing the direction of current flowing through a conductor affect its resistance?
Answer: No, changing the direction of current flowing through a conductor would not affect its resistance. Resistance is a property of the material and its dimensions, not the direction of current flow.
Question 5: If two identical resistors are connected in parallel, what happens to the equivalent resistance of the circuit?
Answer: When two resistors of the same resistance are connected in parallel, the equivalent resistance of the circuit is halved. This is because the total resistance in a parallel circuit is given by the reciprocal of the sum of the reciprocals of individual resistances. For two identical resistors R, the equivalent resistance Rp is given by Rp = R/2.