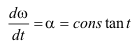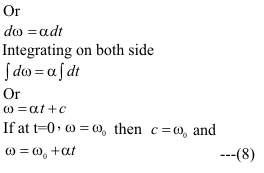Question 1. A wheel initially has an angular velocity of 18 rad/s. It has a constant angular acceleration of 2.0 rad/s2 and is
slowing at first. What time elapses before its angular velocity is 18 rad/s in the direction opposite to its initial
angular velocity?
a 3 sec
b 6 sec
c 18 sec
d none of these
Solution 11
ω
0=18
ω=-18
angular acceleration(α)=-2
Now
ω=ω
0+αt
or t=18