How to solve quadratic equations by completing the square

So far we learned about how to solve quadratic equation by factoring , This page we will learn about Solving quadratic equations by completing the square

Solving quadratic equations by completing the square

In this method we create square on LHS and RHS and then find the value.
ax² +bx+c=0
Step 1 Dividing by a on both the sides
$x^2 +\frac {b}{a} x+\frac {c}{a}=0$

Step 2 Square formation on the LHS using the first two terms. So quadratic equations becomes
$(x+ \frac {b}{2a})^2 - (\frac {b}{2a})^2 + \frac {c}{a}=0$

Step 3 Rearranging the terms on the LHS and RHS,we get the quadratic in the form
$(x+ \frac {b}{2a})^2=\frac {(b^2-4ac)}{4a^2}$

Step 4 Now you can see that RHS does not contain any variable ,it just contains the variables,So we find the square root of the calculated term and RHS to find the roots of the quadratic equation

Geometric Meaning of completing the square

This is explained Geometrically as below

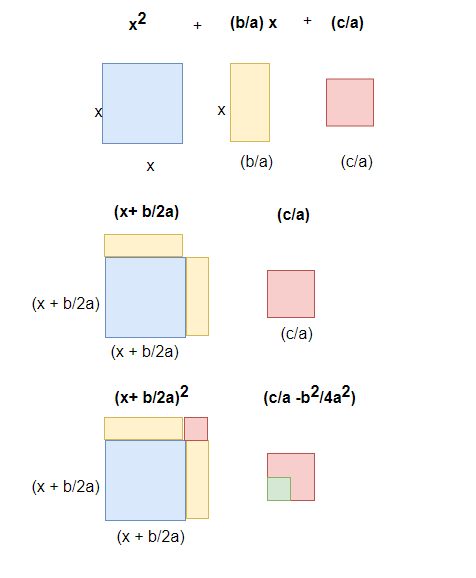
Completing square method Example
Example 1
$x^2 +4x-5=0$
Solution
step 1 Now a=1,so no need to divide
step 2 Square formation on the LHS using the first two terms. So quadratic equations becomes
$(x+2)^2 -4-5=0$
step 3 Rearranging the terms on the LHS and RHS,we get the quadratic in the form
$(x+2)^2=9$
step4 Roots of the equation can be find using square root on both the sides
$x+2 =-3$ => $x=-5$
$x+2=3$ => $x=1$

Example 2
$x^2-9x+20=0$
Solution
step 1 Now a=1,so no need to divide
step 2 Square formation on the LHS using the first two terms. So quadratic equations becomes
$(x-4.5)^2 +20 -20.25=0$
step 3 Rearranging the terms on the LHS and RHS,we get the quadratic in the form
$(x-4.5)^2=.25$
step4 Roots of the equation can be find using square root on both the sides
$x-4.5 =.5$ => $x=5$
$x - 4.5=-.5$ => $x=4$

Example 3
$x^{2} + 4 x - 45 = 0$
Solution
step 1 Now a=1,so no need to divide
step 2 Square formation on the LHS using the first two terms. So quadratic equations becomes
$(x+2)^2 -45-4=0$
step 3 Rearranging the terms on the LHS and RHS,we get the quadratic in the form
$(x+2)^2=49$
step4 Roots of the equation can be find using square root on both the sides
$x+2 =-7$ => $x=-9$
$x+2=7$ => $x=5$

Solve below questions using Completing square method

• $x^{2} - 12 x + 35 = 0$
• $x^{2} - 14 x + 40 = 0$
• $y^{2} - 4 y + 4 = 0$
• $z^{2} - 6 z + 8 = 0$

Answer

• $x = -9, x = 5$
• $x = 5, x = 7$
• $x = 4, x = 10$
• $x = 2$
• $x = 2, x = 4$

---