

We have already known that direct current (DC) is produced by the voltage source whose pole does not change their polarity with time. Hence direction of flow of direct current does not changes with time.
Alternating current on the other hand is produced by voltage source whose terminal polarity keeps alternating with time i.e., terminal which was positive at one instant of time becomes negative sometime later and vice -versa.
Due to changing polarity of voltage source direction of flow of current also keep changing.
In this chapter Alternating Current and Electrical Machines we would learn how voltage and current changing with time are related to each other in various circuits with components namely resistors, capacitor and inductor
An alternating current is that current whose magnitude changes continuously with time and direction reverses periodically
An alternating current is one whose magnitude changes sinusoidal with time. Thus, alternating current is given by
$$I=I_0sin\left(\omega t\right)\tag{1}$$
Or it can also be represented by equation
$$I=I_0cos\left(\omega t\right)$$
Where
$I_0=$ current amplitude or peak value of alternating current.
Both these representations lead to the same result.
If $T$ is the time period of alternating current and $f$ is the frequency, then
$$\omega=\frac{2\pi}{T}=2\pi f \tag{2}$$
Where $\omega$ is called angular frequency of A.C and $\phi$ is known as phase constant. Complete set of variations of the current in one time period T is called cycle.
Instead of sine function AC can also be represented by cosine function and each representation leads to same results. We will discuss circuits with sine representation of A.C
Figure given below shows the contrast between alternating and direct current. It shows the variation of both AC and DC with time.
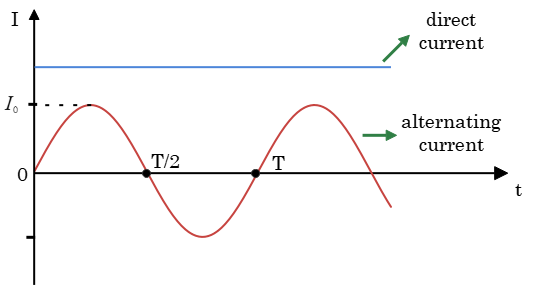
It can clearly be seen from this figure that A.C. rises from 0 to maximum in one direction, then falls to zero at T/2, before rising from 0 to maximum in the opposite direction and dropping to zero again at time T, finishing one complete cycle.
It is important to note here that
Because alternating current is positive in one half of the cycle and negative in the other, its mean value over the entire cycle is zero. It will be proved in a later section of the article.

Full form of alternating emf is alternating electro motive force. Let us now understand the alternating emf meaning by first defining it.
The emf or voltage whose magnitude changes sinusoidal with time is known as alternating emf and is represented by the relation
$$E=E_0sin\left(\omega t\right)\tag{3}$$
Or it can also be represented by
$$E=E_0cos\left(\omega t\right)$$
where $E_0$ is the peak value of alternating emf.
Above equation represents the instantaneous value of alternating emf .
So here, for instance, the magnitude of the EMF changes with time and its direction reverses periodically.
Let us begin our discussion by first looking at how alternating emf is generated? When a coil is rotated in a magnetic field an alternating emf is induced. Relation (1) and (3) gives us the relation for alternating current and alternating emf and shows us how they vary with time.
Now suppose this emf is applied to a electric circuit of resistance $R$. Then current flowing through this circuit will be
$$I=\frac{E}{R}=\frac{E_0}{R}sin\left(\omega t\right)$$
Or,
$$I=I_0sin\left(\omega t\right)$$
This as we know is the relation for AC in the circuit. This equation represent s the instantaneous value of AC.
Here,
$I= $ instantaneous value of alternating current
$I_0=\frac{E_0}{R}=$ the peak or maximum value of alternating current and is also known as the current amplitude.
It is the maximum value attained by alternating current in either direction. It is also known as peak value of current and is denoted by $I_0$.
It is given by the relation $$I_0=\frac{E_0}{R}$$
The time taken by an alternating current to complete one cycle of its variations is called its time period and is denoted by $T$.
$$\text{Time period} = \frac{\text{Angular displacement in a complete cycle}}{\text{Angular Velocity}}$$
Or,
$$T=\frac{2\pi}{\omega}$$
The number of cycles completed per second by an A.C. is called its frequency and is denoted by $f$. $$f=\frac{1}{T}=\frac{\omega}{2\pi}$$
Important Derivation : Prove mathematically that the average value of AC over one complete cycle is zero.
We know that instantaneous value AC at any instant $t$ is given by
$I=I_0 \sin\omega t$
Let us assume that this current is constant through a very small time interval $dt$, then the amount of charge that flows through the circuit in this small time interval $dt$ is,
$dq=Idt=I_0\sin\omega t \cdot dt$
Total charge that flows through the circuit in one complete cycle of AC,
\begin{align*}
q &=\int dq=\int_{0}^{T}I_0\sin\omega t \cdot dt \\
&=I_0\left [ \frac{-\cos\omega t}{\omega} \right ]_{0}^{T}\\
&=-\frac{I_0}{2\pi/T}\left [ \cos \frac{2\pi}{T}t \right ]_{0}^{T}\\
&=-\frac{I_0 T}{2\pi}\left [ \cos 2\pi - \cos 0\right ]\\
&=-\frac{I_0 T}{2\pi}\left [ 1 - 1 \right ]=0
\end{align*}
This proves that the average value of AC over one complete cycle is
$\langle I\rangle_{full\;cycle}=\frac{q}{T}=0$
which is equal to zero.