

Class 12 Physics > Electric Charges and Fields (Chapter 1 Hub Page) > Electric Charge and Basic Properties
This page contains Class 12 Physics notes for Chapter 1: Electric Charges and Fields as per the NCERT / CBSE syllabus. These notes cover the fundamental concepts of electrostatics required for board exams as well as competitive exams like JEE and NEET.
The following topics related to electric charge are discussed in this page:
In the basic properties of electric charge, we study the law of conservation of charge, quantization of charge, and additivity of charges, which are essential ideas in electrostatics.
This chapter forms the foundation for later topics such as electric current, electric field, and magnetism. A clear understanding of these concepts is important for mastering electricity and magnetism in Class 12 Physics.
Electric charge is a fundamental property associated with elementary particles. It accompanies fundamental particles whenever they exist. Electron, proton and neutron are a few examples of fundamental particles.
According to William Gilbert,
The charge is something possessed by material objects that makes it possible for them to exert electrical forces and to respond to electrical force.
We know that in an atom, electrons revolve around a nucleus which has a positive charge.
All matter is made up of atoms. Each atom consists of a small, positively charged nucleus containing protons and neutrons, surrounded by negatively charged electrons revolving in different shells.
In a neutral atom, the total positive charge of the protons is exactly equal to the total negative charge of the electrons. Hence, the atom as a whole is electrically neutral.
When a body is charged by rubbing, contact or induction, electric charge is not created. Charging takes place due to the transfer of electrons from one body to another.
If a body loses electrons, it becomes positively charged due to deficiency of electrons. If a body gains electrons, it becomes negatively charged due to excess of electrons.
This explains why the charge acquired by two bodies on rubbing is always equal in magnitude and opposite in sign.
Electric charge is the property responsible for electric forces acting between the nucleus and electrons in an atom. This electric force binds the atom together.
Charges are of two kinds:
(i) negative charge
(ii) positive charge
In an atom, electrons are particles having negative charge. The nucleus consists of protons and neutrons. Protons have positive charge, while neutrons are electrically neutral. Neutrons are electrically neutral and carry zero charge.
The experiments lead to the fundamental results that:
(1) Like charges repel
(2) Unlike charges attract

The electric force between two electrons is the same as the electric force between two protons kept at the same distance apart; in both cases, the force is repulsive.
The electric force between an electron and a proton placed at the same distance apart is attractive in nature.
The assignment of negative charge to the electron and positive charge to the proton is only a convention. It does not mean that the charge on an electron is smaller than that on a proton.
The importance of electric forces lies in the fact that almost all phenomena in our daily life are governed by them. All matter around us consists of atoms or molecules in which electric charges are exactly balanced.
Note: One coulomb is a very large unit of charge. In most electrostatic phenomena, the charges involved are of the order of microcoulomb ($\mu$C) or nanocoulomb (nC).

There are materials in which electric charges can flow easily, while in other materials charges cannot flow easily. Substances through which electric charges can flow easily are called conductors. All metals like copper, aluminium, etc., are good conductors of electricity.
Substances through which electric charges cannot flow easily are called insulators. Examples of insulating materials are glass, rubber, mica, plastic and dry wood.
The presence or absence of free electrons in a material determines whether it is a conductor or an insulator. Conductors have free electrons which are loosely bound to the nuclei of their atoms. Insulators do not have free electrons; in them, electrons are strongly bound to the nuclei.
It is important to note that:
1. The charge transferred to a conductor gets distributed over its entire surface due to mutual repulsion between like charges.
2. The charge transferred to an insulator remains localised at the point where it is placed.
3. Insulators can be charged, but the charge does not flow freely through them.
Semiconductors form the third class of materials. Their electrical properties lie between those of conductors and insulators. Silicon and germanium are examples of semiconductors.
Note: The electrical conductivity of semiconductors increases with increase in temperature.
Question 1. Why do metals conduct electricity?
Answer. Atoms of metals have outer electrons which are not bound to any one atom. These electrons can move freely throughout the metal lattice and hence conduct electricity.
Case 1: Body has a positive charge
When a body has a positive charge, it means that electrons have been removed from it. As electrons have mass, this results in a slight decrease in the mass of the body. The decrease in mass is equal to the total mass of electrons removed.
Case 2: Body has a negative charge
When a body has a negative charge, it means that electrons have been added to it. This results in a slight increase in the mass of the body. The increase in mass is equal to the total mass of electrons added.
Important Note: During charging, only electrons are transferred; protons remain bound inside the nucleus.
There are three main methods of charging a body:
Rubbing, as the term suggests, involves moving two objects back and forth against each other. One of the simplest ways to experience electric charge is by rubbing certain bodies together.
During rubbing, electrons are transferred from one material to another. As a result, one body acquires a positive charge and the other acquires an equal negative charge. These charges remain on the surfaces of the materials until they are discharged.
For example, when a comb is passed through dry hair, the comb becomes charged and can attract small pieces of paper. This happens because the comb either gains or loses electrons during rubbing. The charged comb then exerts electric force on the neutral paper pieces, resulting in attraction.
Many materials, when rubbed, show this effect and attract light objects such as bits of paper, straw, or feathers.
| Material becoming positively charged | Material becoming negatively charged |
|---|---|
| Glass rod | Silk cloth |
| Woollen cloth or cat skin | Amber, ebonite, rubber rod |
| Woollen carpet | Rubber shoe soles |
| Woollen coat | Plastic seat |
The explanation of charging by rubbing is straightforward. Material bodies normally contain equal numbers of protons and electrons and are electrically neutral. When a glass rod is rubbed with a silk cloth, electrons are transferred from the glass rod to the silk cloth. As a result, the glass rod becomes positively charged and the silk cloth becomes negatively charged.
Charging of a glass rod by rubbing with silk, or a comb by passing it through dry hair, are examples of frictional (static) electricity.
The temporary electrification of a conductor when a charged body is brought near it, without physical contact, is called electrostatic induction.
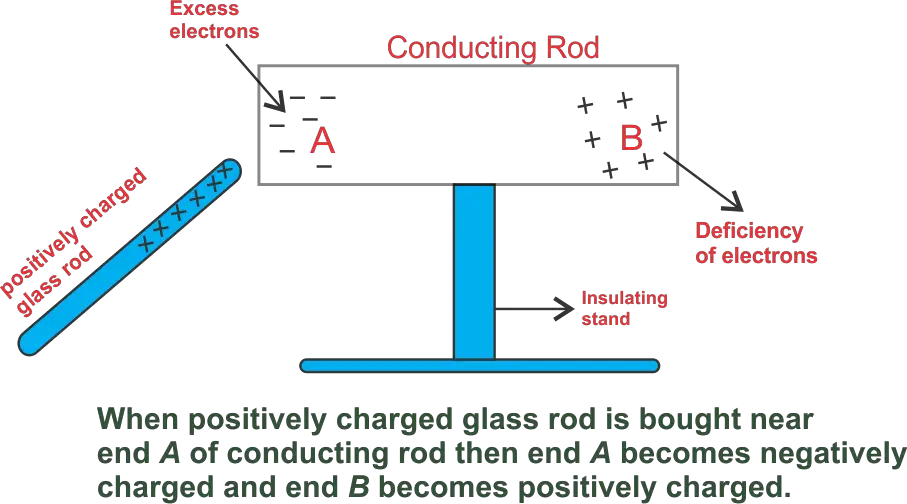
When a charged body is brought near an uncharged conductor, free electrons inside the conductor redistribute themselves due to electrostatic forces. As a result, opposite charges appear on the nearer side and like charges on the farther side.
In this process, there is no transfer of electrons between the charged body and the conductor because there is no physical contact.
Important Note: Charging by induction is possible only for conductors, as free movement of electrons is required.
Charging by conduction occurs when a charged conductor is brought into direct contact with an uncharged conductor.
Because metals have a large number of free electrons, charge flows from one conductor to the other on contact. After separation, both conductors acquire charges of the same nature.
Note: In charging by conduction, the original charged body always loses some charge.
| Charging by Rubbing | Charging by Conduction | Charging by Induction |
|---|---|---|
| Occurs due to friction between two bodies | Occurs due to direct contact | Occurs without physical contact |
| Both bodies acquire charges of opposite nature | Both bodies acquire charges of same nature | Induced charge is opposite in nature |
| Charge appears due to transfer of electrons | Charge appears due to transfer of electrons | No electron transfer between bodies |
| Commonly occurs in insulators | Occurs only in conductors | Occurs only in conductors |
| Earthing is not required | Earthing is not required | Earthing is essential |
| Example: glass rod and silk cloth | Example: touching a charged metal sphere | Example: charging a metal sphere using a charged rod |
Electric charges add up like real numbers, i.e., electric charge is a scalar quantity. If a system has n charges $q_1, q_2, q_3, \ldots, q_n$, then the total charge of the system is given by
Electric charge is a scalar quantity, as it adds algebraically and has no direction.
$$ q = q_1 + q_2 + q_3 + \cdots + q_n $$Proper sign must be used while adding charges.
For example, if
$q_1 = +1\,\text{C}$, $q_2 = -2\,\text{C}$ and $q_3 = +4\,\text{C}$, then
Law of conservation of charge: The algebraic sum of electric charges in an isolated system remains constant.
Note: Conservation of charge is valid in all physical processes, including nuclear reactions.
The elementary charge $e$ is a fundamental constant of nature.
Important Note: At the macroscopic level, charge appears continuous because $n$ is very large.
Conceptual Note: Fractional charges such as $\pm \frac{e}{3}$ and $\pm \frac{2e}{3}$ exist only on quarks, which are not observed in isolation. Hence, all observable charges are always integral multiples of the elementary charge $e$.
These solved examples are related to electric charge and its basic properties.
Question 1. Is there any transfer of mass when electrons are transferred from one substance to another?