When hydrogen gas present on discharge tube passed through high voltage & low pressure, the radiations emitted passed through spectroscope and spectrum is obtained on photographic plate. Hydrogen spectrum contains several lines known as series. The series present in hydrogen spectrum are:-
Balmer showed that wave no. of spectral lines in visible region is given by
Wave no. for any two series is obtained by
is called the Rydberg constant for hydrogen.
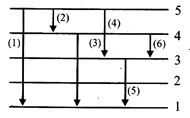
The below shows the Lyman, Balmer and Paschen series of transitions for hydrogen atom
Question 1
Calculate the wavelength of the spectral line in the spectrum of hydrogen tom when n = 3 in Balmer formula.
Solution
$ \frac {1}{\lambda } = R (\frac {1}{(n_1^2}- \frac {1}{n_2^2 })$
For Balmer series n
1=2
$ \frac {1}{\lambda } = R (\frac {1}{(2^2}- \frac {1}{n_2^2 })$
Now for n
1=3
$ \frac {1}{\lambda } = R (\frac {1}{(2^2}- \frac {1}{3^2 })$
λ= 36/5 R = 6.792 × 10
-5 cm
Question 2
In hydrogen atom the electron jumps from 3rd orbit to 1st orbit. Find out fequency & wavelenght of spectrum line.
Solution
$ \frac {1}{\lambda } = R (\frac {1}{(n_1^2}- \frac {1}{n_2^2 })$
$ \frac {1}{\lambda } = R (\frac {1}{(1^2}- \frac {1}{3^2 })$
$ \frac {1}{\lambda }=109677 (1- \frac {1}{9})$
λ= = 9/8 × 1/(1.09 × 10
5 )
= 1.02 × 10
-5 cm.= 102 × 10
-5 m
Now, C =
νλ
ν=(3 × 10
8)/(102 × 10
-5 )
=(3 × 10
13)/102
= 2.67 × 10
11 s
-1
Question 3
What is the wavelength of light emitted when the electron in a hydrogen atom undergoes transition from an energy level with n = 4 to an energy level with n = 2?
Solution
λ= ?
n = 4, n = 2
$ \frac {1}{\lambda } = R (\frac {1}{(n_1^2}- \frac {1}{n_2^2 })$
$ \frac {1}{\lambda } = R (\frac {1}{(2^2}- \frac {1}{4^2 })$
? = 16 / 109678 × 3 cm = 486 nm
Question 4
Calculate the wave number for the longest wavelength transition in the Balmer series of atomic hydrogen.
Solution
$ \frac {1}{\lambda } = R (\frac {1}{(n_1^2}- \frac {1}{n_2^2 })$
For Balmer series n
1=2
$ \bar{\nu}=\frac {1}{\lambda } = R (\frac {1}{(2^2}- \frac {1}{n_2^2 })$
To get maximum wavelength, wave no. must be least. For wave no. to be least n
2 should be minimum
Therefore n
2 = 3
$ \bar{\nu} = R (\frac {1}{(2^2}- \frac {1}{n_2^2 })$
$\bar{\nu} = 1.09 \times 10^5 \times 5/36 = 1.5 \times 10^4$ cm
-1
Question 5
Which of the following is true
(a) Lyman series is a continuous spectrum
(b) Paschen series is a line spectrum in the infrared
(c) Balmer series is a line spectrum in the ultraviolet
(d) The spectral series formula can be derived from the Rutherford model of the hydrogen atom
Solution
Answer is (b)
Question 6
In a collection of H-atoms, all the electrons jump from n = 5 to ground level finally (directly or indirectly), without emitting any line in Balmer series. The number of possible different radiations is:
(a) 10
(b) 8
(c) 7
(d) 6
Solution
(d)