A set of four quantum numbers which specify the energy, size, shape and orientation of an orbital about all the electrons present in an atom is called Quantum Numbers. To specify an orbital only three quantum numbers are required while to specify an electron all four quantum numbers are required.
The number of orbitals in a subshell = 2l + 1. For a given value of n, l can have n values ranging from 0 to n-1. Total number of subshells in a particular shell is equal to the value of n.
It gives information about the No. of preferred orientations of electrons in sub – shell. Each orientation corresponds to orbital
gives no. of orbitals in a sub shell
It refers to orientation of the spin of the electron. It can have two values +1/2 and -1/2. +1/2 identifies the clockwise spin and -1/2 identifies the anti- clockwise spin.
Question 1
(a) How many subshell are possible with n = 4
(b) How many e- will be present in subshell having ;m
s = -1/2 for n = 4.
Solution
For n = 4
l = 0 to (n – 1)
= 0, 1, 2, 3
l = 0 m
l = -l to + 1 =0
l = 1 m
l = -l to + l =-1, 0, 1
l = 2 m
l = -l to + l = -2, -1, 0, 1, 2
l=3 m
l = -l to + l = -3, -2, -1, 0, 1, 2, 3
For m
s =-1/2 there will be 16 electrons
Question 2
Which of the following set of quantum no. is impossible?
a) n = 3, l = 2, m = -2, s = +1/2
b) n = 4, l = 0, m = 0, s = +1/2
c) n = 3, l = 2, m = -3, s = +1/2
d) n = 5, l = 3, m = 0, s = +1/2
Solution
Answer is (c)
n = 3
l = 0 to (n – 1)
= 0 to 2
0, 1, 2
s, p, d
m = -l to + l
l = 0 m
l = -l to + 1 =0
l = 1 m
l = -l to + l =-1, 0, 1
l = 2 m
l = -l to + l = -2, -1, 0, 1, 2
Question 3
What is the total number of orbitals associated with the principal quantum number n = 3 ?
Solution
For n = 3, the possible values of l are 0, 1 and 2.
Thus there is one 3s orbital (n = 3, l = 0 and ml = 0)
There are three 3p orbitals (n = 3, l = 1 and ml = -1, 0, +1)
There are five 3d orbitals (n = 3, l = 2 and ml = -2, -1, 0, +1+, +2).
Therefore, the total number of orbitals is 1+3+5 = 9
The same value can also be obtained by using the relation; number of orbitals
= $n^2$, i.e. 32 = 9.
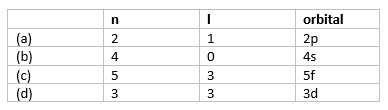
Question 4
Using s, p, d, f notations, describe the orbital with the following quantum numbers
(a) n = 2, l = 1
(b) n = 4, l = 0
(c) n = 5,l = 3
(d) n = 3, l = 2
Solution