

In this page, we will learn about electrical force, the definition of electric force along with a few examples. At the end of the page, we will also define electrostatic force.
Electric force is one of the interactions among particles we observe in nature. The very nature of matter depends on these electrical forces. Four basic interactions occurring between elementary particles are
At this present level, you are familiar with gravitational forces. We will explore what are electric forces. It is the force of attraction that acts between all particles(or bodies) having mass. So, if we have two bodies of mass $m_1$ and $m_2$ kept at a distance $r$ from each other then from Newton's law of gravitation,
$$F_{12}=G \frac{m_1 m_2}{r^2}$$where $G$ is Universal Gravitational Constant. Above equation gives the magnitude of force exerted by $m_1$ on $m_2$. Mass $m_2$ also exert an equal and opposite force mass $m_1$. From the above equation, we can see that Gravitational forces are inverse square in nature. It decreases inversely as the square of the distance between the two masses.
The electric force also varies inversely as the square of the distance between charge. It is billions of time stronger than the gravitational force. From the description of electric charges, we know that there are two kinds of charged matter. One is positive and another one is negative. We also know that like charges repel and unlike charges attract each other. Gravitational interaction in contrast only attract masses which are kept at a distance from each other. On atomic and molecular level gravitational forces play no role. This is because electric forces are very strong. The electric repulsion between two protons is $10^35$ times stronger than the gravitational interaction between them.
Now if you try to bring a bunch of positive charges together they would repel with an enormous force. They will then spread out in all directions. The same thing happens with negative charges.
What if you try to bring even mixture of positive and negative charges? The answer is they would be pulled together by an enormous force of attraction. If the net amount of positive and negative charges in the mixture is equal then these forces would balance and mixture becomes neutral.

These forces (explained above) acting between charges are Electrical forces. The force on a charged particle due to the electric field in its vicinity is the electric force.
All matter we see around us consists of positive protons and negative electrons. They are attracting and repelling each other with electric force. In matter around us, these electrical forces balance out so perfectly that we did not feel any force at all. The electric field - and hence the electric force - can change over time, if the charge particles generating the field are moving. An electric field does not have to be static.
Electromagnetic interactions involve moving charges. It includes both electric and magnetic forces. We already learned about electric forces. Magnetic forces are forces acting between magnets. It occurs between a magnet and a piece of iron. These are the result of electric charges in motion. So, both electric and magnetic phenomenon can be derived from charged particles.
Strong interactions are responsible for holding the nucleus of an atom target. It counters the repulsion between protons in a nucleus. The range of weak interactions is very short. Weak interaction between sub-atomic particles causes radioactive decay and thus plays an important role in nuclear fission (see reference).
There is much electric force example that we came across in our day to day life. Some are
(a) Woolen clothing:-(b) Adhesive forces of glue associated with surface tension, all are electric in nature
(c) Forces behind lightning that strikes from the cloud base to the ground are electric in nature.
If all the charged particles under observation are stationary, then the corresponding force on the charged particles is an electrostatic force. If certain electrical insulator materials are rubbed electrostatic charge is developed on them. We discussed it under topic charging by rubbing.
Figure below shows a concept map explaining what are electrostatic forces
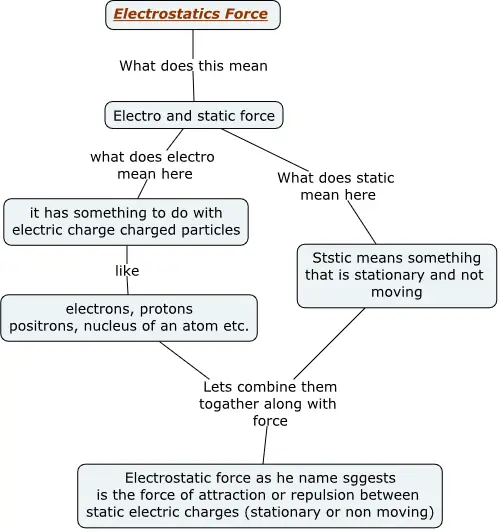
In the next page, we will learn about how to calculate the electrostatic force between two charged bodies using Coulomb's Law.