

Average velocity vector is given as
$<\mathbf{v}>=\frac{\int \mathbf{v}dt}{t}$
Now given
$\mathbf{r}=a cos(kt)\mathbf{i}+b sin(kt)\mathbf{j}$
or
$\mathbf{v}= \frac {d\mathbf{r}}{dt}= - a sin(kt)\mathbf{i} + b cos(kt)\mathbf{j}$
Now we calculate Average velocity vector as
$<\mathbf{v}>=\frac{\int (- a sin(kt)\mathbf{i} + b cos(kt)\mathbf{j})dt}{t}$
$<\mathbf{v}>= \frac {a cos(kt)\mathbf{i}+ b sin(kt)\mathbf{j}}{t}$
The situation is depicted in the figure below
Let take v as the velocity with respect to wind. Lets it makes an angle $\theta$ with the east direction
Velocity of the airplane with respect to ground=2000/40=50 km/hr
From the figure
$vsin \theta =5$
and $vcos \theta =50$
So $v= \sqrt {2525}$ and $\theta = tan^{-1} \frac {1}{10}$
Let us assume
$u_{12}$= Speed of second car with respect to first car
$u_{21}$= Speed of first car with respect to second car
also $u_{12}= u_{21}$
From the figure given below and from mathematics theorem
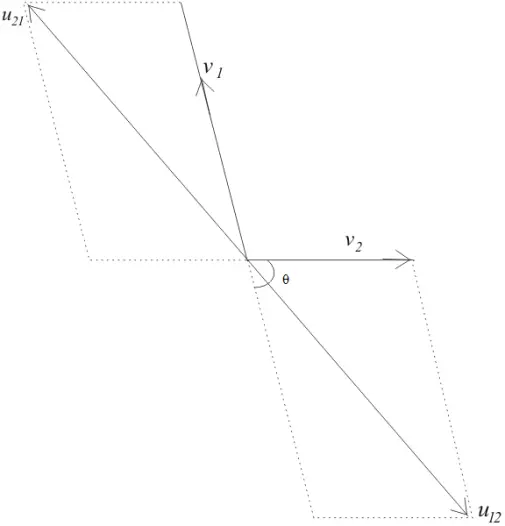
$u_{12}= \sqrt {u_1^2 + u_2^2 + 2u_1 u_2 cos \theta}$
Now time will given by
$t = \frac {s}{\sqrt {u_1^2 + u_2^2 + 2u_1 u_2 cos \theta}}$
Choosing for the X-axis the vertical line of motion OY with the origin at O , we see from the figure that the displacement x of the end Y is given by the equation
$x = \sqrt {l^2 - (v_0 t)^2 }$
$x^2 = l^2 - v_0^2 t^2 $
$x^2 + v_0^2 t^2 = l^2$
or
$\frac {x^2}{l^2} + \frac {t^2}{(l\v_0)^2} = 1 $
This is the equation of an ellipse.
Now
$\mathbf{v_1^{'}} = \mathbf{v_1} + \mathbf{a}t_0$
Multiplying by $m_1$ on both sides
$m_1 \mathbf{v_1^{'}} = m_1 \mathbf{v_1} + m_1 \mathbf{a}t_0 $ ----(1)
Similarly
$m_2 \mathbf{v_2^{'}} = m_2 \mathbf{v_2} + m_2 \mathbf{a}t_0 $ ----(2)
$m_3 \mathbf{v_3^{'}} = m_3 \mathbf{v_3} + m_3 \mathbf{a}t_0 $ ----(3)
Adding (1) ,(2) and (3)
$ \frac {(m_1 \mathbf{v_1} + m_2 \mathbf{v_2} + m_3 \mathbf{v_3}) - (m_1 \mathbf{v_1^{'}} + m_2 \mathbf{v_2^{'}} + m_3 \mathbf{v_3^{'}})}{m_1 + m_2 + m_3} = - \mathbf{a}t_0$
Adding (1) and (2) only
$ \frac {(m_1 \mathbf{v_1} + m_2 \mathbf{v_2} ) - (m_1 \mathbf{v_1^{'}} + m_2 \mathbf{v_2^{'}} )}{m_1 + m_2 } = - \mathbf{a}t_0$
Now we have
$\mathbf{v_1^{'}} = \mathbf{v_1} + \mathbf{a}t_0$ -- (4)
$\mathbf{v_2^{'}} = \mathbf{v_2} + \mathbf{a}t_0$ -- (5)
$\mathbf{v_3^{'}} = \mathbf{v_3} + \mathbf{a}t_0$ --(6)
Adding (4),(5) and (6)
$ \frac {(\mathbf{v_1} + \mathbf{v_2} + \mathbf{v_3}) - (\mathbf{v_1^{'}} + \mathbf{v_2^{'}} + \mathbf{v_3^{'}})}{3} = - \mathbf{a}t_0$
Subtracting (4) and (6)
$ \mathbf{v_1^{'}} - \mathbf{v_2^{'}} = \mathbf{v_1} - \mathbf{v_2}$
Position of X after time t
$\mathbf{r_1}=(-3 + 2t)\mathbf{i}$
Position of Y after time t
$\mathbf{r_2}=(-3 + 3t)\mathbf{j}$
Relative vector of Y w.r.t to X
$= \mathbf{r_2} - \mathbf{r_1}$
Or =$(3t -3) \mathbf{j} + (3-2t) \mathbf{i}$
Let x be the distance of ring X from Fixed point A
Let y be the distance of ring Y from fixed point A'
Let L is distance between the two rods
Now length of the string remains constant
$ x + \sqrt {L^2 + (y-x)^2 } = C$
So, it is vertically upwards
Now velocity of Ring Y with respect to Ring X
$w_x = w -v = v - \frac {v}{cos \theta} -v = - \frac {v}{cos \theta}$
It is also vertically upwards
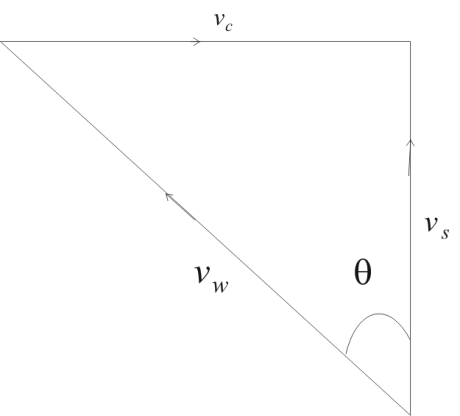
Let $v_c$ -> Velocity of the current
$v_w$ -> Velocity w.r.t current
$v_s$ -> Velocity w.r.t shore
Now
$\mathbf{v_w}=\mathbf{v_s} - \mathbf{v_c}$
$\mathbf{v_s}= \mathbf{v_w} + \mathbf{v_c}$
To directly cross the river
$ \mathbf{v_s} \perp \mathbf{v_c}$
$ sin \theta = \frac {v_c}{v_w} = \frac {5}{10} = \frac {1}{2}$
So $\theta = 30$°
So angle made with the current is 90+30=120 °
$v_s = v_w cos \theta = \frac {10 \sqrt {3}}{2}= 5 \sqrt {3} $ m/s
$t = \frac {d}{v_s} = \frac {50}{5 \sqrt {3}} = \frac {10}{ \sqrt {3}} $ seconds
Hence (d) is the correct answer

Here (a) is the answer as solved above
Here (a) is the answer as solved above
To maximize the components of his velocity perpendicular to the river bank, the swimmer should head straight across the stream
Hence (a) is the correct option
T=50/10=5 sec
$D=v_c \times t=5 \times 5=25 $m/s
For these, it is clear that all the four options are correct
$y=x^2$ -(1)
$v_x=\frac {dx}{dt}=3 $
Differentiating equation (1) w.r.t time
$ \frac {dy}{dt} = 2x \frac {dx}{dt}$
$ \frac {dy}{dt} = 2x \times 3 =6x$
So, at x=1/3
$ \frac {dy}{dt} = 2x \times 3 =6x =2$
$\frac {dx}{dt}=3 $
So, Magnitude and direction will be
$ \sqrt {13} ,tan^{-1} \frac {2}{3}$
$ \frac {dy}{dt} =6x$
$\frac {dx}{dt}=3 $
Differentiating equations w.r.t time
$ \frac {d^y}{dt^2}= 6 \frac {dx}{dt} = 18$
$ \frac {d^x}{dt^2}=0$
So magnitude and direction will be
18 m/sec2 ,900