

Given $\mathbf{R}= (Asin \omega t)\mathbf{i} + (Acos \omega t)\mathbf{j}$
So $x= Acos \omega t$ => $ cos \omega t =\frac {x}{A}$
$y=Asin \omega t$ => $sin \omega t =\frac {y}{A}$
Now we know that
$Sin^ 2 \omega t+ cos^2 \omega t =1$
So, $(\frac {x}{A})^2+ (\frac {y}{A})^2=1$
Or, $x^2+y^2=A^2$
Which is a equation of a circle
Given $\mathbf{R}= (Asin \omega t)\mathbf{i} + (Acos \omega t)\mathbf{j}$
At t=0
$\mathbf{R}= A \mathbf{i}$
At $t= \frac {2 \pi}{\omega }$
$\mathbf{R}= A\mathbf{j}$
Now average velocity=$ \frac {Displacement}{t} = \frac {A\mathbf{j}-A \mathbf{i}}{\frac {2 \pi}{\omega }} =\frac {2A \omega}{\pi} (\mathbf{j}-\mathbf{i})$
Given $\mathbf{R}= (Asin \omega t)\mathbf{i} + (Acos \omega t)\mathbf{j}$
$\mathbf{v}= \frac {d\mathbf{R}}{dt}$
$= (-A \omega sin \omega t)\mathbf{i} + (A \omega cos \omega t)\mathbf{j}$
$\mathbf{a}= \frac {d\mathbf{v}}{dt}$
$=(-A \omega ^2 cos \omega t)\mathbf{i} + (-A \omega ^2 sin \omega t)\mathbf{j}$
$\mathbf{a}.\mathbf{v} = [(-A \omega sin \omega t)\mathbf{i} + (A \omega cos \omega t)\mathbf{j}]. [(-A \omega ^2 cos \omega t)\mathbf{i} + (-A \omega ^2 sin \omega t)\mathbf{j}]$
=0
We know from above
$\mathbf{a}= \frac {d\mathbf{v}}{dt}$
$=(-A \omega ^2 cos \omega t)\mathbf{i}+ (-A \omega ^2 sin \omega t)\mathbf{j}$
$=-A \omega ^2 \mathbf{R}$
So it means acceleration directed towards the radial direction
So, tangential acceleration is zero.
Same as above
Radial acceleration= $A \omega ^2$
Given $\mathbf{R}= (Asin \omega t)\mathbf{i} + (Acos \omega t)\mathbf{j}$
At t=0
$\mathbf{R}= A\mathbf{i}$
At $t = \frac {\pi}{ \omega}$
$\mathbf{R}= -A\mathbf{j}$
So displacement= $-2A\mathbf{i}$
Distance =Distance traveled on the half circle = $\pi A$

Velocity of A=$u\mathbf{i}$
Velocity of B =$-u\mathbf{j}$
Velocity of B w.r.t to A=Velocity of B-Velocity of A =$-u(\mathbf{i}+\mathbf{j})$
Velocity of A=$u\mathbf{i}$
Velocity of B ==$-u\mathbf{j}$
Velocity of A w.r.t to B=Velocity of A-Velocity of B
=$u(\mathbf{i}+\mathbf{j})$
Position vector of A =$ut\mathbf{i}$
Position vector of B=$-ut\mathbf{j}$
Relative position vector of particle A wrt to B at time t=Position vector of A - Position vector of B =$ut(\mathbf{i}+\mathbf{j})$
(a) Let us draw the displacement diagram
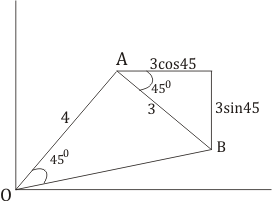
From the diagram, it is clear for position A
$x_a =4 \times (cos 45)=2.83$ Km
$y_a =4 \times (sin 45) =2.83$ Km
Now taking components of AB vector across horizontal and vertical direction
$x=3cos45=2.12$ km
$y=3sin45=2.12$ km
From the figure
$x_b = x_a+x=2.12+2.83=4.95$ km
$y_b=y_a-y=2.83-2.12=.71$ km
(b) Distance of Point B from the origin is given by
$= \sqrt {x_b^2 + y_b^2}$
=5 km
(c) Position vector of point A = $x_a \mathbf{i} + y_a\mathbf{j} = 2.83 \mathbf{i}+2.83 \mathbf{j}$
Position vector of point B =$x_b \mathbf{i} + y_b \mathbf{j} = 4.95 \mathbf{i} +.71 \mathbf{j}$
(a) and (b)
Horizontal component of velocity
$v_{0x}=v_0 cos 40=15.3$ m/sec
Vertical component of velocity
$v_{0y}=v_0 sin40=15.3$ m/sec
Now let take t be the time in which it strike the wall.
Then
$ x= v_{0x}t$
$y= v_{0y}t-\frac {gt^2}{2}$
Now x=8 m
So $8=15.3 \times t$
Or t=.52 sec
Now
$y= v_{0y}t- \frac {gt^2}{2}$
Substituting all the values
Y=5.33 m
(c) Horizontal velocity will remain same during all the motion while vertical velocity will have downward acceleration of g.
So Horizontal component of velocity at the point of strike
$v_x =15.3$ m/sec
Vertical component of velocity at the given point
$v_y =v_{0y}-gt=12.8 - (9.8)(.52)=7.704$ m/sec
a. Given
$\mathbf{R}= (2sin2 \pi t)\mathbf{i} + (3cos2 \pi t)\mathbf{j} $
So co-ordinates of the particles are
$x=2sin2 \pi t$ or $sin2 \pi t =\frac {x}{2}$
$y=3cos2 \pi t$ or $cos2 \pi t =\frac {y}{3}$
Now we know that
$(sin2 \pi t)^2+ (cos2 \pi t)^2=1$
So
$(\frac {x}{2})^2 + (\frac {y}{3})^2 =1$
Or
$ \frac {x^2}{4} + \frac {y^2}{9} =1 $
This is an equation of an ellipse
So the trajectory of the particle is an ellipse
(b) Given
$\mathbf{R}= (2sin 2 \pi t)\mathbf{i} + (3 cos 2 \pi t)\mathbf{j} $
Velocity vector is given by
$\mathbf{v} = \frac {d\mathbf{R}}{dt}$
or
$\mathbf{v} = (4 \pi cos 2 \pi t) \mathbf{i}+ (-6 \pi sin 2 \pi t)\mathbf{j}$
Acceleration vector is given by
$\mathbf{a} = \frac {d\mathbf{v}}{dt}$
Or
$\mathbf{a}= (-8 \pi ^2 sin 2 \pi t ) \mathbf{i}+(-12 \pi ^2 cos 2 \pi t)\mathbf{j}$
$=-4 \pi ^2 \mathbf{R}$
Also it indicates that acceleration is towards the center at every point of the motion.
(c)Magnitude of velocity is given by
$v = \sqrt {v_x^2 + v_y^2}$
or
$v= \sqrt {16 \pi ^2 cos^2 2 \pi t + 36 \pi ^2 sin^2 2\pi t}$
$= 2 \pi \sqrt {4 cos^2 2 \pi t + 9 sin^2 2\pi t}$
$=2 \pi \sqrt { 9 - 5 cos^2 2 \pi t}$
As $( sin2 \pi t )^2+( cos2 \pi t )^2=1$
So $v_{max} will occur at times when $| cos2 \pi t |=0$
Or $2 \pi t=(2n+1) (\pi /2)$ where n=0,1,2.....
Or t=1/4,3/4,5/4 ....
Also value of $v_{max} =6 \pi $
Now $v_{min} will occur at times when $| cos2 \pi t |=1$
Or $2 \pi t=n \pi $ where n=0, 1,2 ......
Or t=0,1/2,1.....
Also value of $v_{min} =4 \pi$
(d)
(e)Now when t=0 , $cos \alpha =0$
or $ \alpha =90$ °
When t=1/4 , $cos \alpha =0$ or 90°
(a) The situation is depicted the figure below.
Now we know that, the trajectory of the ball is given by
$y= (tan \theta) x - \frac {gx^2}{2v_0^2 cos^2 \theta}$
Now here $ \theta = 60$ so $tan \theta= \sqrt {3}$ and $cos \theta = \frac {1}{2}$
Or $y=(\sqrt {3} )x - \frac {2gx^2}{v_0^2}$ ---(1)
Now the equation of the slope is given by
$y=x tan \theta$
Now here $ \theta = 30$ so $ tan \theta = \frac {1}{\sqrt {3}}$
So, $y= \frac {x}{\sqrt {3}}$ ---- (2)
Now the point of strike is the point of intersection of the equation (1) and (2)
Or
$\frac {x}{\sqrt {3}} = (\sqrt {3} )x - \frac {2gx^2}{v_0^2}$
or
$x= \frac {v_0^2}{g \sqrt {3}}$
Now distance along the slope is given by
$x=S cos30$
or $S= \frac {x}{cos30}$
$=\frac {2 v_0^2}{3g}$
(b) Time to reach the point is given by
$x=v_{0x} t$
=> $t= \frac {v_0 cos60}{x}$
=> $ t= \frac {2v_0}{g \sqrt {3}}$
(c) Height above the point O can be found by the equation (2)
$y= \frac {x}{\sqrt {3}}$ ---- (2)
We know that
$x= \frac {v_0^2}{g \sqrt {3}}$
So $y= \frac {v_0^2}{3g}$
(d)Horizontal velocity will remain same throughout the motion as there is no acceleration
$v_x= v_0 cos 60=v_0 / 2$
$v_y =v_{0y}-gt = v_0 sin60-g \times ( \frac {2v_0}{g \sqrt {3}} ) = \frac {-v_0}{2\sqrt {3}}$
So velocity of strike
$ v = \sqrt {v_x^2 + v_y^2} = \frac {v_0}{ \sqrt {3}}$
(a) As given in the question velocity vector of particle is
$\mathbf{v}=a \mathbf{i}+bx \mathbf{j}$
From this we have x and y components of velocity i.e.
and $v_x = \frac {dx}{dt}=a $ and $v_y = \frac {dy}{dt} = bx$ ------- (1)
From equation 1 we can calculate equation describing motion of particle along x and y axis. Thus integrating for x
$\int_{0}^{x} dx = a \int_{0}^{t} dt$
or $x=at$ ------ (2)
Now from equation 2 we have
$dy = bx dt = bat dt$
Integrating it we get
$\int_{0}^{y} dy = ab \int_{0}^{t} t dt$
Or
$y = \frac {1}{2} abt^2$ --------- (3)
From equations 2 and 3 we get
$y = \frac {b}{2a} x^2 $ -------- (4)
This is the required equation of particle's trajectory.
(b) Radius of curvature of trajectory y(x) is given as
$ R= \frac {[1 + (\frac {dy}{dx})^2]^{3/2}}{\frac {d^y}{dx^2}}$ ------ (5)
Differentiating path given in equation 4 for its first and second derivatives we find
and $ \frac {dy}{dx} = \frac {b}{a} x$ and $ \frac {d^2y}{dx^2} =\frac {b}{a}$ -------- (6)
Using equation 5 and 6 we find radius of curvature of trajectory as following
$R = \frac {a}{b} [ 1 + (\frac {b}{a} x)^2 ] ^{3/2}$
Let H be the height of the tower
Now equation of trajectory is
$y=x tan \theta (1- \frac {x}{R})$
Now Range is given as $a_2$
when $y=H ,x=a_1$
so, $H=a_1 tan45(1- \frac {a_1}{a_2}) =\frac {a_1(a_2-a_1)}{a_2}$
The situation is depicted in fig
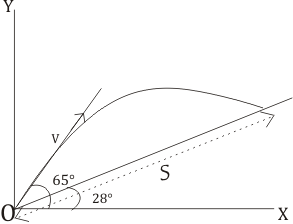
$v_0=33$ m/s and $ \theta _0=65$
The equation of trajectory of the
$y_b=(tan \theta _0)x-\frac {gx^2}{2v_0^2 cos \theta _0}$
or
$y_b=2.14x-.025x^2$
The equation of the incline
$y_i=(tan28)x=.53x$
When the ball strike the incline
$y_b=y_i$
or
$.53x=2.14x-.025 x^2$
or x=64.4 m
The distance along the incline obeys
$x=Scos28$ or $S=72.9$ m
The time to reach that point is given by
$x=v cos65 t$
or
t=4.63 sec
The time taken to reach the pole is given
$R=v_0 cos? t$
or $t= \frac {R}{v_0 cos \theta}$
Now equation of motion of vertical motion
$h=v_0 sin \theta t- \frac {1}{2}gt^2$
at $t= \frac {R}{v_0 cos \theta}$, $h=H$
so
$H=(v_0 sin \theta ) \times ( \frac {R}{v_0 cos \theta}) - \frac {1}{2} g( \frac {R}{v_0 cos \theta}^2$
or $H=R tan? - \frac {gR^2}{2v_0^2 cos^2 \theta}$
Let us take point A from which the boat departs as the origin of the coordinates system. The direction of the axis are shown below in Figure
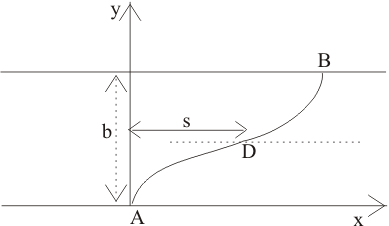
The boat moves in a direction perpendicular to the current at constant velocity u.
Let us take a point B on the boat path which is at a distance y from bank. y< b/2
The current velocity will be
$ v= \frac {2v_0 y}{b}$ ---(1)
Now time taken to reach the boat at this point B
$t= \frac {y}{u}$
or $y=ut$
Substituting this value in equation (1)
$ v= \frac {2v_0 ut}{b}$
The velocity of the boat with respect to ground
=Velocity of the boat with respect to river + velocity of river with respect to ground
$\mathbf{v}= \frac {2v_0 ut}{b} \mathbf{i} + u \mathbf{j}$
Differentiating it
$ \mathbf{a} = \frac {2v_0 u}{b} \mathbf{i}$
This will be the acceleration
Now the boat will reach middle point in time
$T= \frac {b}{2u}$
The horizontal distance travelled during this time
$s = \frac {aT^2}{2}$
Or,
$s= \frac {v_0 b}{4u}$
Now let take the velocity for y > b/2
The current velocity will be
$v= \frac {2v_0(b- y)}{b} $ --- (1)
Then
$\mathbf{v}= \frac {2v_0(b- y)}{b} \mathbf{i} + u \mathbf{j}$
Differentiating it
$ \mathbf{a} = -\frac {2v_0 u}{b} \mathbf{i}$
Now the boat will reach bank
$T= \frac {b}{2u}$
The horizontal distance travelled during this time
$s = ut + \frac {aT^2}{2}$
$s = u \frac { b}{u} - \frac {2v_0 u}{2b} (\frac { b}{u})^2$
$s = \frac {v_0 b}{4u}$
So total distance
$s = \frac {v_0 b}{2u}$
Now we know from above calculation for y< b/2
$y=ut$
$x = \frac {at^2}{2}$
Now $a= \frac {2v_0u}{b}$
Substituting this in above
$x = \frac {v_0 u_0}{b} t^2 $
Now $t= \frac {y}{u}$
So
$y^2 = \frac {bu}{v_0} x$
This is a parabola