Here are Multiple Choice Questions(More than one correct) for Projectile motion problems with detailed solution.
Recommended way is to solve them on your own and then check solutions for correctness
Question 1
A ball is projected upward at a certain angle with the horizontal .which of the following statement is/are correct. At highest point
a. velocity of the projectile is not zero
b. acceleration of the projectile is zero
c. velocity of the projectile is along the horizontal direction
d. Acceleration of the projectile is vertically upwards
At highest point vertical component of velocity becomes zero but horizontal components remains.
Net velocity is along horizontal
Also acceleration is vertically downwards throughout the journey
Hence the correct option is (c)
Question 2
Which of the following remains constant during the motion of the projectile fired from a planet,
a. KE
b. Momentum
c. Vertical component of the velocity
d. Horizontal component of the velocity
Since velocity is changing, KE and momentum is not constant.
Now since acceleration is vertically downwards, vertical component of velocity is changing.
Since there is no acceleration is horizontal direction, horizontal components is constant
Hence the correct option is (d)
Question 3
Which one is wrong for a body having uniform circular motion?
a. Speed of the body is constant
b. Acceleration is directed towards the centre
c. Velocity and Acceleration vector are having an angle 45
d. none of the above
Speed of particle is constant in uniform circular motion
Velocity vector is tangent to the path at any point on the path.
Acceleration vector is directly inwards towards center
So velocity and acceleration vector are perpendicular to each other in Uniform circular motion
Hence the answer is (a) and (b)
Question 4.
The range of the projectile depends upon
a. Angle of the projection
b. Acceleration due to gravity
c. Mass of the projectile
d. magnitude of the velocity of projection
$R=\frac {u^2sin 2 \theta}{2g}$
So it depends on velocity, angle and acceleration due to gravity
Hence the answer is (a),(b) and (d)
Question 5.
Two bullets A and B are fired horizontally with speed v and 2v respectively. Which of the following is true
a. Both will reach the ground in same time
b. Bullet with speed 2v will cover more horizontal distance on the ground
c. B will reach the ground in less time than A
d. A will reach the ground in less time than B Solution
Time taken to reach the ground depends on the velocity in vertical direction...Since both the bodies are projected horizontally. There are no vertical components of velocity involved. So they will reach the ground in same time. Now time taken is same so body with more horizontal velocity will travel more on the ground.
Hence the answer is (a) and (b)
Question 6.
A body is projected horizontally from a point above the ground.The motion of body is defined as
$x=2t$
$y=2t^2$
where x and y are horizontal and vertical displacement respectively at time t.Which one of the following is true
a. The trajectory of the body is a parabola
b. The trajectory of the body is a straight line
c. the velocity vector at point t is 2i+4tj
d. the acceleration vector at time t is 4j Solution
Given
x=2t
y=2t2
Eliminating t we get
y=x2/2
So it is parabola
Vx=dx/dt=2
vy=dy/dt=4t
So velocity at any time t is given by
v=2i+4tj
Now similarly
ax=dVx/dt=0
ay=dVy/dt=4
So acceleration vector is a=4j
Hence Answer is (a),(c) and (d)
Question 7.
The initial velocity of the particle is u=4i+3j m/s. It is moving with uniform acceleration a=.4i+.3j m/s2.which of the following is true
a. the magnitude of the velocity after 10 sec is 10m/s
b. The velocity vector at time t is given by (4+.4t)i +(3+.3t)j
c. the displacement at time t is (4t+.22)i +(3t+.152)j
d . None of the above Solution
Given
u=4i+3j m/s
a=.4i+.3j m/s2
So velocity vector at any time t
v=u+at = 4i+3j+(.4i+.3j)t =(4+.4t)i+(3+.3t)j
So velocity at 10 sec
v=8i+6j
|v|=10
displacement vector at any time t
s=ut+(1/2)at2 =(4i+3j)t+(1/2)(.4i+.3j)t2 =i(4t+.2t2)+j(3t+.15t2)
Hence Answer is (a) and (b)
Question 8.
Two projectile A and B are having trajectory equation
$y=a_1x-b_1x^2$ and $y=a_2x-b_2x^2$
If the range is same for both the projectile A and B then which of the following option is true Solution
For projectile A
$y=a_1x-b_1x^2$
for y=0
$x=0$ and $x=\frac {a_1}{b_1}$
Similarly for Projectile B
$y=a_2x-b_2x^2$
for y=0
$x=0$ and $x=\frac {a_2}{b_2}$
For the range to be same
$\frac {a_1}{b_1} =\frac {a_2}{b_2} $
Question 9.
When the projectile is at the highest point of its trajectory, the direction of its velocity and acceleration are
a. parallel to each other
b. anti parallel to each other
c. Inclined to each other at 45
d. Perpendicular to each other
At the highest point of projectile, vertical components of velocity becomes zero. So there are only horizontal components so, net velocity is horizontal at this point. Now acceleration is vertically downwards throughout the motion. So acceleration and velocity vector are perpendicular to each other at highest point
Question 13
The horizontal and vertical displacement of the projectile at time t are
$x=36t$
$y=48t-4.9t^2$
where x and y are in meters and t in second. Initial velocity of the projectile in m/s
a. 15
c. 30
b. 45
d. 60
This question can be solved in two ways
Method 1:
Given
$x=36t$
$y=48t-4.9t^2$
For a body projected with velocity u at an angle $ \theta$ with the horizontal ,the x and y displacement is given by
$x=(ucos \theta)t$
$y=(usin \theta )t-\frac {gt^2}{2}$
Comparing this the given equation we have
$ucos \theta=36$
$usin \theta=48$
Squaring and adding we get
$u^2(cos^ \theta +sin^2 \theta)=3600$
so u=60 m/s
Method 2:
Given
$x=36t$
$y=48t-4.9t^2$
$v_x=\frac {dx}{dt}=36$
$v_y=\frac {dy}{dt}=48-9.8t$
So intial velocity can be found substituting t=0 in both the equation
$v_x=36$
$v_y=48$
So net velocity= $\sqrt {362+482)}=60 $ m/s
Question 14.
It is possible to project an body with a given speed in two possible ways so that it has a same horizontal range. The product of time taken by it in tow possible ways is
a. $ \frac {R}{g}$
b. $ \frac {2R}{g}$
c. $ \frac {3R}{g}$
d. $ \frac {4R}{g}$
If a body is projected with a given velocity u at angle $\theta$ and $(90- \theta)$ to the horizontal, it will have same range R given by
$ R=\frac {u^2 sin2 \theta}{g}$
The corresponding times if flight are
$t_1=\frac {2usin \theta}{g}$
$t_2=\frac {2usin(90- \theta)}{g}= \frac {2ucos \theta}{g}$
$t_1t_2=\frac {2u^2(2sin \theta cos \theta)}{g^2} =\frac {2u^2 sin2 \theta} {g^2}=\frac {2R}{g}$
Question 15.
A projectile has a range R and time of flight T. If the range is tripled by the increasing the speed of the projection, without changing the angle of projection then the time of the flight will become
a $ \frac {T}{\sqrt {3}}$
b $T \sqrt {3}$
c.$ \frac {T}{3}$
d. $3T$
Range is given by
$R=\frac {u^2 sin 2 \theta}{g}$ ----1
and time taken by
$T=\frac {2usin \theta}{g}$ ----2
Now
$3R=\frac {u_c^2 sin2 \theta }{g}$ ---3
$T_c=\frac {2u_c sin \theta }{g}$ ---4
Dividing 1 by 3
$ \frac {1}{3}=(\frac {u}{u_c})^2$ ----5
Dividing 2 by 4
$\frac {T}{T_c}=\frac {u}{u_c}$ ---6
From 5 and 6
$\frac {T}{T_c}=\frac {1}{ \sqrt {3}}$
$T_c=\frac {T}{ \sqrt {3}}$
Question 16.
A large number of stones are fired in all the direction with same speed V.The maximum area of the ground on which this stone will spread is
a. $ \frac {\pi V^4}{g^2}$
b. $ \frac {\pi ^2V^4}{g^2}$
c. $ \frac {\pi V^4}{g}$
d. $ \frac {\pi V}{g^2}$
Range is given by
$R=\frac {v^2 sin2 \theta }{g}$
Range will maximum when $sin2 \theta =1$
So $R= \frac {v^2}{g}$
Now $area= \pi R^2$
$=\frac { \pi v^4}{g^2}$
Question 17.
A body is projected horizontally from the top of the building 39.2 m high. How long will it take to hit the ground
a. 2 sec
b. 4 sec
c. 1 sec
d. $2 \sqrt {2}$ sec Solution
Initial vertical component of velocity is zero
so $h=\frac {1}{2}gt^2$
$39.2=(\frac {1}{2} \times 9.8 \times t^2$
$t=2 \sqrt {2}$ sec
Question 18
A boy throws a ball with such an initial velocity and at such an angle of elevation, so that the range is r and maximum height to which ball rises is h. find the maximum range that can be obtained with same initial velocity Solution
Now from Projectile motion
$h= \frac {v_0^2 sin^2 \alpha}{2g}$ ---(1)
And
$r= \frac {v_0^2 sin 2 \alpha}{g}$ ---(2)
Also maximum Range $R_m$
$R_m = \frac {v_0^2}{g}$ ---(3)
Substituting the values of $R_m$ in (1) and (2)
$2h = R_m sin^2 \alpha$ --(4)
$r = R_m sin2 \alpha$ ---(5)
Equation (4) can be rewritten in the form
$h = \frac {R_m}{4}(1 - cos 2 \alpha)$
$ cos 2 \alpha = 1 - \frac {4h}{R_m}$
Equation (5) can be rewritten in the form
$ sin 2 \alpha = \frac {r}{R_m}$
Now
$ sin^ 2 2\alpha + cos ^2 2\alpha=1$
$ (\frac {r}{R_m})^2 + (1 - \frac {4h}{R_m})^2 =1$
Or, $R_m=2h + \frac {r^2}{8h}$
Question 19.
An airplane is moving with a horizontal velocity v at a height h above a level plane.If a projectile is fired from an gun at an instant when the plane is vertically above the gun, what is the minimum initial velocity of the projectile in order to hit the plane. Solution
It is evident; we must have horizontal velocity of projectile equal to horizontal velocity of the airplane.
So
$v_0 cos \alpha = v$ ---(1)
If the projectile has to ever attain the height h, then vertical component of projectile must be greater then $\sqrt {2gh}$
So
$v_0 cos \alpha \geq \sqrt {2gh}$ ---(2)
Squaring equation 1 and 2 .And then adding it
$v_0^2 \geq v^2 + 2gh$
$v_0^2 \geq \sqrt { v^2 + 2gh}$
Question 20.
An aero plane is moving in the sky and a bag is dropped from t he plane. Let a and v denote the acceleration and velocity of the aero plane. Consider two cases
a is constant and non zero
a is zero and plane is moving with uniform velocity
Match the following:-
(P) The trajectory of bag in case A w.r.t. ground is
(L) Parabola
(Q) The trajectory of bag in case B w.r.t. plane is
(M) straight line
(R) The trajectory of bag in case B w.r.t. ground is
(N) no appropriate match
(S) The trajectory of bag in case A w.r.t. plane is
With $ a \neq 0$ With respect to plane
$ \frac {d\mathbf{v}}{dt} = \mathbf{g} -\mathbf{a}$ which is a constant acceleration
Now since $v_0=0$ with respect to plane.
So it is a straight line With Respect to ground
$v \neq 0$ at t=0
Acceleration =$\mathbf{g}$
So it is a parabola
With a=0 and $v \neq 0$ With respect to plane
$ \frac {d \mathbf{v}}{dt} =\mathbf{g}$ which is a constant acceleration
Now since $v_0=0$ with respect to plane.
So it is a straight line With Respect to ground
$v \neq 0$ at t=0
Acceleration =g
So it is a parabola
Question 21.
An object under goes an projectile motion starting from origin with initial velocity
Under acceleration due to gravity
Hm -> Maximum height reached by object
R -> Range of the object
Match the column
Column A
Column B
A) tan of angle between velocity and x axis at any point of time
B) tan of projection angle θ0 for a projectile at origin
C) Range of the projectile
D) tan of the angle of position vector at any time
(A) A plank of length L is moving in the direction of x-axis in the X-Y plane. A point A is located on the left hand side of the plank. Position of point A at t=0 is (L,0). The plank is moving in the right direction with velocity v Question 22.
A person standing at point A at t=0 throws a stone with velocity v and at an angle 600 with X axis. Find the co-ordinates of the maximum height reach by the stone Solution
Question 23.
Find the velocity vector at the maximum height if i and j are the unit vectors along X and Y axis respectively Solution
At maximum height ,Y components of velocity becomes zero, So X components remains only
So $\mathbf{v} =\frac {3}{2}v \mathbf{i}$
Question 24.
Find the co-ordinates of the stone where its hit the X-axis Solution
Total time when the stone hit X-axis =2 × Time to reach maximum height
$ T = \frac {2v}{g} \frac {\sqrt {3}}{2}$
or
$T= \frac {v \sqrt {3}}{g}$
Distance travelled along X -axis in this time will be given as
$=\frac {3}{2}v \times \frac {v \sqrt {3}}{g} = \frac {3 \sqrt {3}}{2} \frac {v^2}{g}$
So, co-ordinates are $ L + \frac {3 \sqrt {3}}{2} \frac {v^2}{g}, 0$
Question 25.
Find the velocity vector of the stone when it hits X-axis. Solution
When the stone hit the X-axis, The horizontal velocity will remain same while the vertical components of the velocity will be downward direction
$ \frac {3}{2}v \mathbf{i} - frac {\sqrt {3}}{2}v \mathbf{j}$
Question 26.
Find the co-ordinates of the point A on the plank when the stone hit the X-axis Solution
Total time
$T= \frac {v \sqrt {3}}{g}$
So distance travelled $= \frac {v^2 \sqrt {3}}{g}$
So co-oridinates are
$L + \frac {v^2 \sqrt {3}}{g}, 0$
Question 27.
Find the maximum value of velocity v so as to land the stone on the plank Solution
(B)An object is fired up on the inclined place of angle $\alpha$ . The object is fired with velocity $v_0$ and angle of elevation $\theta$ with the horizontal Question 28.
Find the range on the inclined plane Solution
Consider the figure given below and writing the equation for point X
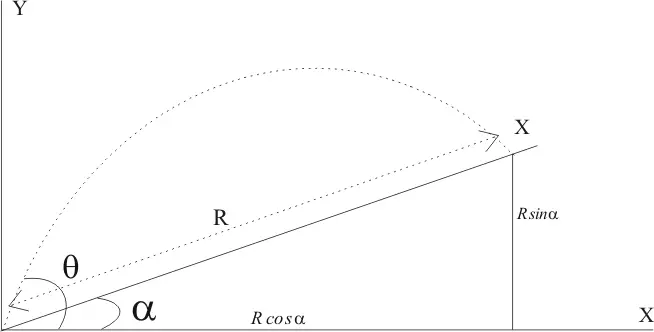
$x = (v_0 cos \theta) t = R cos \alpha$ - (1)
$y = (v_0 sin \theta)t - \frac {1}{2} gt^2= R sin \alpha $ -(2)
Eliminating t between equation (1) and (2),we get
Question 29.
Find the relation between $\theta $ and $\alpha$ for which object will have maximum range Solution
Now for R to be maximum
$ sin (2 \theta - \alpha)=1$
$ tan 2 \theta + cot \alpha=0$
Question 30.
A stone is thrown from ground level over horizontal ground. It just clears three walls, the successive distances between them being r and 2r. The inner wall is 15/7 times as high as the outer walls which are equal in height. The total horizontal range is nr, where n is an integer. Find n
a. 2
b. 3
c. 4
d. 5 Solution
Let us just assume that both the outer walls are equal in height say \(h\) and they are at equal distance \(x\) from the end points of the parabolic trajectory as can be shown below in the figure.
Now equation of the parabola is
\(y = bx - c{x^2}\)-- (1)
\(y = 0\) at \(x = nr = R\)
where \(R\) is the range of the parabola.
Putting these values in equation (1) we get
\(b = cnr\) -- (2)
Now the range \(R\) of the parabola is
\(R = a + r + 2r + a = nr\)
This gives
\(a = \left( {n - 3} \right)\frac{r}{2}\) -- (3)
The trajectory of the stone passes through the top of the three walls whose coordinates are
\(\left( {a,h} \right),\left( {a + r,\frac{{15}}{7}h} \right),\left( {a + 3r,h} \right)\)
Using these co-ordinates in equation 1 we get
\(h = ab - c{a^2}\) -- (4)
\(\frac{{15}}{7}h = b(a + r) - c{(a + r)^2}\) --(5)
\(h = b(a + 3r) - c{(a + 3r)^2}\) ----(6)
After combining (2), (3), (4), (5) and (6) and solving them we get n = 4.
link to this page by copying the following text Also Read
