|
|
|
Rotation
(1) Introduction
- In this chapter, we will study about the special kind of motion of a system of particles that is rotation
- We see examples of rotational motion in our everyday life for example rotation of earth about its own axis create the cycle of day and night .Motion of wheel, gears ,motors, planet ,blades of the helicopter etc are all the example of rotational motion
- To understand the rotational motion as a whole we are first required to understand the concept of angular position, velocity, acceleration, centripetal acceleration
- Till now in our study of dynamics we have always analyzed motion of an object by considering it as a particle even when the size of the object is not negligible
- In this process we represent object under consideration as a point mass and shape and size of the object remains irrelevant while discussing the particular problem under consideration
- But this point mass or point particle model is inadequate for problems involving rigid body motion i.e. rigid body undergoing both translational and rotational motion
- As an example consider the motion of a wheel, we cannot consider a wheel as a single particle because different parts of the wheel in motion has different velocities and acceleration
- Here in this chapter we will consider rigid bodies having definite shape and size and are capable of having both rotational and translational motion
- The rigid body is a body with a perfectly defined and unchanging shape that is no matter how the body moves, the distance between any two particles within the body remains constant
- Although the way we define rigid body gives us the definition of an idealized rigid body and real materials always deforms on the application of force and this idealized rigid body assumption can be used freely for the substances where deformation is negligibly small and can be neglected
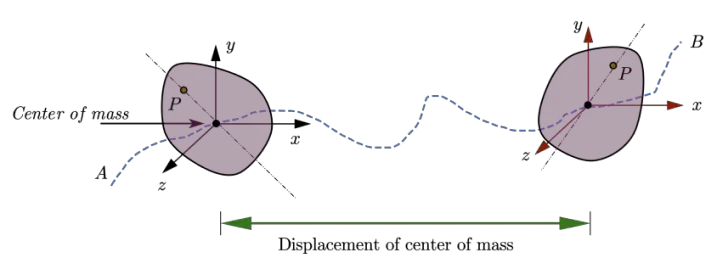
- Motion of a rigid body in general can be considered to consist of a translation of center of mass of the body plus rotation of the body about an axis through the center of mass as shown below in the figure
- In this chapter we will concentrate on the simplest kind of rotation that is the rotation of the rigid body about the fixed axis
(2) Angular velocity and angular acceleration
- Consider a rigid body of arbitrary shape rotating about a fixed axis through point O and perpendicular to the plane of the paper as shown below in the figure-1
FIG
- while the body is rotating each and every point in the body moves in a circle with their center lying on the axis of rotation and every point moves through the same angle during a particular interval of time
- Consider the position of a particle say ith particle at point P at a distance ri from point O and at an angle θi which OP makes with some reference line fixed in space say OX as shown below in the figure
- If particle moves an small distance dsi along the arc of the circle in small amount of time dt then
dsi=vidt ----(1)
where vi is the speed of the particle
- dθ is the angle subtended by an arc of length dsi on the circumference of a circle of radius ri,so dθ( in radians) would be equal to the length of the arc divided by the radius
i.e.
dθ=dsi/ri =vidt/ri ----(2)
- distance dsi would vary from particle to particle but angle dθ swept out in a given time remain same for all the particles i.e. if particle at point P moves through complete circle such that
dθ=2π rad
Then all the other particles of the rigid body moves through the angular displacement dθ=2π
- So rate of change of angle w.r.t time i.e. dθ/dt is same for all particles of the rigid body and dθ/dt is known as angular velocity ω of the rigid body so
ω=dθ/dt ----(3)
- Putting equation (3) in equation (2) we find
vi=ri(dθ/dt) =riω ---(4)
This shows that velocity of ith particle of the rigid body is related to its radius and the angular velocity of the rigid body
- Angular velocity of a rotating rigid body can either be positive or negative. It is positive when the body is rotating in anticlockwise direction and negative when the body id rotating in clockwise direction
- Unit of angular velocity radian per second (rad-s-1) and since radian is dimensionless unit of angle so dimension of angular velocity is [T-1]
- Instead of radians angles are often expressed in degrees. So angular velocity can also be expressed in terms of degree per second and degree per minute
- we know that
2π radians =3600
or π radians/1800=1
And this relation can be used for expressing angular velocity in degree to that of angular velocity in terms of radian
- Angular acceleration is the rate of change of angular velocity w.r.t time. Thus for rigid body rotating about a fixed axis
- Unit of angular acceleration is radian /sec2
- Angular acceleration holds not only for that rotating rigid body but also for the each and every particle of that body
- Differentiating equation (4) w.r.t to t we find
where ai=ait=riα is the tangential component of linear acceleration of a point at a distance ri from the axis
- Each particle in the rigid body also has the radial linear acceleration component v2/r ,which can also be expressed in terms of an of angular velocity i.e.
and this acceleration aic pointing inwards towards the radial line is also known as centripetal acceleration
NEXT
|
Related Articles
|
Competition Resources
|
|
|
