Class 10 Maths Worksheet for Polynomials

$x^2 + x -12$
$= x^2 + 4x -3x -12$
$=x(x+4) -3(x+4) = (x-3)(x+4)$
So zeroes are 3 and -4

for $f(x)=x^2 + 7x + 7$
we get
$a+b=-7$
$ab=7$
Now
$a^{-1} + b^{-1}-2ab$
$= \frac {a+b-2a^2b^2}{ab}$
$= \frac {-7-98}{7}=-15$

Given $p(x) =x^3 - ax^2 + 6 - a$
By remainder theorem
p(a) = 6-a

for $f(x)=x^2 - 5x + k$
we get
$p+q= 5$
$pq=k$
Now
$p -q = 1$
$(p -q)^2=1$
$(p+q)^2 -4pq=1$
$25-4k=1$
$k=6$

Two zeroes = 0, 0
Let the third zero be k.
The, using relation between zeroes and coefficient of polynomial, we have:
$k + 0 + 0 = -\frac {b}{a}$
Third zero = k = -b/a

Let $f(x)=x^2 + (a + 1) x + b$
Then
$2-3= - (a+1) or a=0$
$-6 = b$
So a=0 and b=6

$k_1 k_2 k_3 = - \frac {Constant term}{Coefficient \; of \; x^3}$

Hence
$k_1 k_2 k_3 =-c$
Now $k_1=-1$
So,
$k_2 k_3=c$

Let $f(x)=x^3-6x^2 + 8x$
Method -1
$=x(x^2 -6x +8)=x(x-2)(x-4)$
So 0,2,4 are zeroes of the polynomial. or a=2 and b=2 or -2
Method -2
$k_1 + k_2 + k_3 = - \frac {Coefficient \; of \; x^2}{Coefficient \; of \; x^3}$

$a-b + a + a+b=6$ or a=2
Now $k_1 k_2 k_3 = - \frac {Constant term}{Coefficient \; of \; x^3}$
$(2-b)2(2+b) =0$ or b=+2 or -2

$f(x) = 2x^2 - 7x + 3$
$=2x^2 -x -6x+ 3= x(2x-1) -3(2x -1) = (x-3)(2x-1)$
So zeroes are 3 and 1/2
Now
$a^2 + b^2$
$ =9 + \frac {1}{4}= \frac {37}{4}$

$4x^2 + 12x + 9$
$=4x^2 + 6x + 6x + 9$
$= 2x(2x+ 3) + 3(2x + 3)=(2x+3)^2$
So p=-3/2 and q=-3/2
So, $p -1= -\frac {5}{2}$ and $q -1= -\frac {5}{2}$
So quadratic polynomial will be
$(x + \frac {5}{2})^2$
or
$4x^2 + 20x + 25$

Let $f(x) =2x^3 + x^2 -5x + 2$
For Verification of zeroes, we can simply substitute in the polynomial and verify
$f(1/2) = 2 (\frac {1}{2}}^3 + (\frac {1}{2})^2 -5 \frac {1}{2} + 2 = 0$
$f(1) = 2(1)^3 + (1)^2 -5(1) +2 =0$
$f(2) = 2(2)^3 + (2)^2 -5(2) +2 =0$
The relationship between the zeroes and coefficient is given by
i. $k_1 + k_2 + k_3 = - \frac {Coefficient \; of \; x^2}{Coefficient \; of \; x^3}$
or
$\frac {1}{2} + 1 -2 = -\frac {1}{2}$
$-\frac {1}{2} = -\frac {1}{2}$
Verified

ii. $k_1 k_2 k_3 = - \frac {Constant term}{Coefficient \; of \; x^3}$
$ \frac {1}{2} \times 1 \times (-2) = -1$
$-1=-1}
Verified

iii. $k_1 k_2 + k_2 k_3 + k_1 k_3 = \frac {Coefficient \; of \; x}{Coefficient \; of \; x^3}$
$ \frac {1}{2} -2 -1 = \frac {-5}{2}$
$ \frac {-5}{2}= \frac {-5}{2}$
Verified

for $f(x)=x^2 - (k + 6)x + 2(2k - 1)$
We get,
$p+q = k+6$
$pq = 2(2k-1)$
Now
$2(p+q) =pq$
Therefore,
$2(k+6) = 2(2k-1)$
or $k+6=2k-1$
or $k=7$

for $f(x)=ax^2 - 5x + c$
we get
$m+n=\frac {5}{a}$
$mn=\frac {c}{a}$
Given $m + n = m \times n = 10$
Therefore,
5/a=10
a=1/2

c/a=10
or c=5

$k_1 + k_2 = \sqrt {2}$
$k_1 k_2 = -\frac {3}{2}$
Now the quadratic polynomial is given by
$x^2 -(k_1 + k_2) x + k_1 k_2$
$=x^2 -\sqrt {2} x -\frac {3}{2}$
or
$=2x^2 -2 \sqrt {2} x -3$
Now we need to find the zeroes of this polynomial
$2x^2 -2 \sqrt {2} x -3$
$=2x^2 -3 \sqrt {2} x + \sqrt {2}x -3$
$= \sqrt {2}x( \sqrt {2}x -3) + 1( \sqrt {2}x -3)$
$=(\sqrt {2}x +1)(\sqrt {2}x -3)$
or roots are $-\frac {1}{\sqrt {2}} , \frac {3}{\sqrt {2}$

$k_1 + k_2 + k_3 = - \frac {Coefficient \; of \; x^2}{Coefficient \; of \; x^3}$
$ a+a+b +a +2b = 6$ or $a+b= 2$ or $a =2-b$
Now
$k_1 k_2 k_3 = - \frac {Constant term}{Coefficient \; of \; x^3}$
$a(a+b)(a+2b) =-10$
$2(2-b)(2+b)=-10$
$(4-b^2) =-5$
or b= -3 or 3
So a= 5 or -1
The zeroes with a=5 ,b=-3 can be expressed as 5 ,2,-1
The zeroes with a=-1 ,b=3 can be expressed as -1 ,2,5

Here is the division

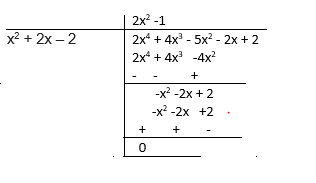
So $ f(x) = (2x^2 -1) g(x)$

Let a be one zero ,then another will be 2a
Now
$a + 2a= \frac {5}{2}$ or a= 5/6
Also
$a \times 2a = \frac {-(2k+1)}{2}$
or
$\frac {25}{9} = -(2k+1)$
$2k = -\frac {34}{9}$
or
k= -17/9

for $f(x) = x^2 - px + q$
We get
$m+n=p$
$mn=q$
a. $m^2+ n^2=(m+n)^2 -2mn= p^2-q$
b. $m^{-1} + n^{-1} = \frac {m+n}{mn} = \frac {p}{q}$

Let a-b,a ,a+b are the zeroes
Now
$k_1 + k_2 + k_3 = - \frac {Coefficient \; of \; x^2}{Coefficient \; of \; x^3}$
$a -b +a +a +b= 12$ or a=4
Also
$k_1 k_2 + k_2 k_3 + k_1 k_3 = \frac {Coefficient \; of \; x}{Coefficient \; of \; x^3}$
$(a - d)a + a(a + d) + (a + d)(a - d) = 39$
$3a^2 - d^2 = 39$
Substituting the value of a from above
$3(4)^2 - d^ = 39$
$d = \pm 9$
hence, series are 1 , 4 , 7 or 7, 4 , 1

now,
$k_1 k_2 k_3 = - \frac {Constant term}{Coefficient \; of \; x^3}$

$7 \times 4 \times 1 = -k$
k=-28

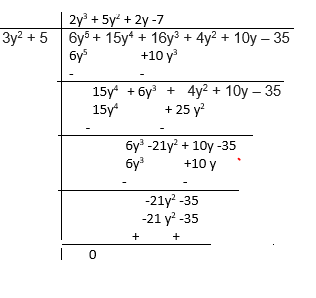
Dividend = Divisor X Quotient + Remainder
Dividend - Remainder = Divisor X Quotient
Dividend - Remainder is always divisible by the divisor.

Now, it is given that f(x) when divided by x² -2x + k leaves (x + a) as remainder.
So f(x) -(x+a) is divided by x² -2x + k

x⁴ -6x³ + 16x² - 25x + 10 -(x+a) =x⁴ -6x³ + 16x² - 26x + 10 -a

Now doing the division

Now remainder should be zero
(-10 + 2k)x + (10 - a - 8k + k²) = 0
-10 + 2k = 0 or k=5

Now (10 -a - 8k + k²) = 0
or 10 - a - 8 (5) + 5² = 0
or - a - 5 = 0
a =-5

√2 , -√2, 2,1

k= -3
The other root is 3/2

61x - 65

4q+10+r=0 -(1)
q/4 +5/2 +r=0 or q+10+4r=0 -(2)
Subtracting 1 from 2
3q-3r=0
q=r

For x² + 2x + k is a factor of polynomial 2x⁴ + x³ - 14x² + 5x + 6, it should be able to divide the polynomial without any remainder


Comparing the coefficient of x we get.
21+7k=0 or k=-3

So x² + 2x + k becomes x² + 2x -3 = (x-1)(x+3)
Now
2x⁴ + x³ - 14x² + 5x + 6= (x² + 2x -3)(2x²-3x-8+2k)
=(x² + 2x -3)(2x²-3x-2)
=(x-1)(x+3)(x-2)(2x+1)
or x= 1,-3,2,=-1/2

x² - x +1

By cubic polynomial equation, we have
a+b+c=-p
ab+bc+ac=q
abc=-2

Now given ab+1=0 or ab=-1
So abc=-2
(-1)c=-2 or c=2

2p + q + 5
=-2(a+b+c) +(ab+bc+ac) +5
=-2(a+b+2) +[-1+2(a+b)] +5
=-4 -1+5=0