

First download this acceleration worksheet with answers as pdf. Try to solve problems on your own and then you can check the answers.
Download this assignment ad pdf Download
Solution:- Given in the question that
$x=18t+5t^2$
(i) we know that velocity
\begin{align*}
v &=\frac{dx}{dt} \\
& =\frac{d}{dt}(18t+5{{t}^{2}}) \\
& =18+10t \\
\end{align*}
To find velocity at $t=2s$, put $t=2$ in above equation.
So, Instantaneous velocity$=18+10\times 2=38m.{{s}^{2}}$
(ii) displacement at $t=2$ is
${{x}_{1}}=18\times 2+5\times {{2}^{2}}=56m$
At $t=3$
${{x}_{2}}=18\times 3+5\times {{3}^{3}}=54+45=99m$
average velocity
$v=\frac{{{x}_{2}}-{{x}_{1}}}{{{t}_{2}}-{{t}_{1}}}=\frac{99-56}{3-2}=43m{{s}^{-1}}$
(iii)
$a=\frac{dv}{dt}=\frac{d}{dt}(18+10t)=10m{{s}^{-2}}$.
Solution :-
(i) let the car accelerate for the time $t$, and $v$ be the maximum velocity of the car at time $t_1$.
We know that
$v =u+at$
Therefore, $v =0+\alpha t_1$
or,
$t_1=\frac{v}{\alpha} \qquad \qquad (1)$
Now starting with maximum velocity $v$, the car decelerates at constant rate $\beta$ and comes to rest in time $(t-t_1)$. Therefore,
$0=v-\beta (t-t_1)$
or,
$t-{{t}_{1}}=\frac{v}{\beta }\qquad \qquad (2)$
Adding equations (1) and (2)
$t = \frac{v}{\alpha} + \frac{v}{\beta} = v\left( {\frac{{\alpha + \beta }}{{\alpha \beta }}} \right)$
or,
$v = \frac{{\alpha \beta t}}{{\alpha + \beta }}\qquad \qquad (3)$
This gives maximum velocity attained by the car.
(ii) distance covered by the car in time $t_1$ is
${{x}_{1}}=0+\frac{1}{2}\alpha t_{1}^{2}$
By using equation of motion
$x=ut+\frac{1}{2}a{{t}^{2}}$
${{x}_{1}}=\frac{1}{2\alpha }\cdot {{v}^{2}}=\frac{-{{v}^{2}}}{2\alpha }$
[using 1]
Distance travelled by the car in time $\left( t-{{t}_{1}} \right)$
\begin{align*}
x&=v (t-{{t}_{1}})-\frac{1}{2}\beta {{(t-{{t}_{1}})}^{2}} \\
& = v\cdot \frac{v}{\beta}-\frac{1}{2}\beta\frac{v^2}{\beta^2}=\frac{v^2}{2\beta}\\
\end{align*} (using epn2)
Therefore total distance travelled by the car is
\begin{align*}
x&={{x}_{1}}+{{x}_{2}}=\frac{{{v}^{2}}}{2\alpha }+\frac{{{v}^{2}}}{2\beta } \\
& =\frac{{{v}^{2}}}{2}\left [ \frac{1}{\alpha }+\frac{1}{\beta } \right ] \\
\end{align*}
Using equation (3) and solving for x we get
$$x=\frac{\alpha \beta {{t}^{2}}}{2(\alpha +\beta )}$$
Solution:-
Here $u=0, \, t=25 s$,
Given that
$v=180\, Km/h=\frac{180\times 5}{18}=50\, m/s$
Acceleration
$a=\frac{v-u}{t}=\frac{50-0}{25}=2\frac{m}{s^2}$
Distance,
\begin{align*}
s&=ut+\frac{1}{2}a{{t}^{2}} \\
& =0\times 25+\frac{1}{2}\times 2\times {{(25)}^{2}} \\
& =625m. \\
\end{align*}
Solution :-
(i) Here it is given that
$s=2m, \, t = 4s, \, u =0$
as
$s=ut+\frac{1}{2}at^2$
Putting respective values we get
$2=0+\frac{1}{2}\times a\times 4^2$
or,
$a=0.25m/s^2$
(ii) Time taken to cover the first metre of track is given by
$1 = 0 + \frac{1}{2} \times 0.25\times t^2$
$ \Rightarrow {t^2} = 8$
Or $t = 2\sqrt 2 = 2 \times 1.414=2.83 s $
Hence time taken to cover the second meter of track is
$= 4-2.83 = 1.17 s.$
(iii) Speed at the bottom,
$v = u + at = 0+0.25\times 4 = 1m/s$

Question 1- What do you understand by term acceleration and retardation distinguish between average acceleration and instantaneous acceleration.
Question 2- Represent graphically and explain the motion of an object when the object is under the following conditions
(i) object is at rest
(ii) object with uniform motion along straight line
(iii) object with accelerated motion along straight line
(iv) object with decelerated motion moving along a straight line.
Choose correct option to answer following questions.
Question 1 :- A body is covering distance in proportion to square of time. The acceleration of the body is
(a) increasing
(b) decreasing
(c) zero
(d) constant
Answer:- (d)
Question 2:- The relation between $t$ and distance $x$ is $t=\alpha x^2+\beta x$. Where $\alpha$ and $\beta$ are constants.
The retardation is
(a) $2\alpha v^3$
(b) $2\alpha \beta v^3$
(c) $2\beta v^3$
(d) $2\beta ^2 v^3$
Answer :- (a)
Given that
\begin{align*}
t=\alpha x^2+\beta x
\\
\frac{dt}{dt}=2\alpha x\frac{dx}{dt}+\beta \frac{dx}{dt}
\\
1=2\alpha xv+\beta v\\
v\cdot (2\alpha x+\beta )=1\\
(2\alpha x+\beta) =\frac {1}{v}
\end{align*}
Again differentiating both the sides w.r.t. $t$ we get
\begin{align*}
2\alpha \frac {dx}{dt}=-v^{-2}\cdot \frac {dv}{dt}\\
2\alpha v=-v^{-2}\cdot acceleration
\end{align*}
$\Rightarrow \, acceleration\,=\,- 2\alpha v^3$
Hence,
$retardation \, =+2\alpha v^3$
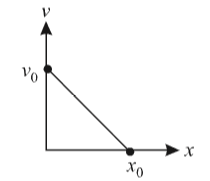
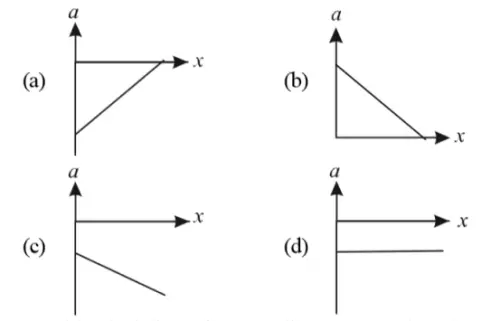
Solution : - (a)
From the given velocity-displacement graph,
$slope=\frac{{{v}_{0}}}{{{x}_{0}}}$ ,
and intercept on y-axis is$v_0$
Thus equation for this graph will be
\begin{align*}
v&=\frac{-v_0}{x_0}x+v_0\,\, \left[ y=mx+c \right]
\\
\frac{dv}{dt}&=-\frac{v_0}{x_0}\frac{dx}{dt}
\\
a&=-\frac{v_0}{x_0}.v
\\
&=-\frac{v_0}{x_0}\left[ -\frac{v_0}{x_0}x+v_0 \right]
\\
&=\frac{v_{0}^{2}}{x_{0}^{2}}x-\frac{v_{0}^{2}}{x_0}
\end{align*}
From this we can clearly see that graph must have positive slope $\left( \frac{{v_0}^{2}}{x^2}\right)$ and negative intercept $\left( -\frac{v_{0}^{2}}{x_0} \right)$ on y-axis.
Solution :- (c)
For accelerated motion
$u=0,\, a = f\, and \, s = s$.
As,
$v^2-u^2=2as$
$\therefore$ $v_{1}^{2}-0^2=2fs$
or,
$v_1=\sqrt{2fs}$
For uniform motion
$u=v_1=\sqrt{2fs}, \, t=t$
Distance travelled,
$s_2=ut=\left( \sqrt{2fs} \right) t$
For decelerated travelled
$u=\sqrt{2fs}, \, a=-f/2, \, v=0$
As, $v^2-u^2=2as$
$0^2-\left( \sqrt{2fs} \right) ^2=2\times \left( -f/2 \right) s_3$
distance travelled,
$s_3=2s$
given in the question total distance travelled is
$s+s_2+s_3=5s$
$s+\left( \sqrt{2fs} \right) t+2s=5s$
or,
$\sqrt{2fs}t=2s$
Squaring both sides me get
$s=\frac{1}{2}ft^2$
Answer :- (c)
\begin{align*}
a=\frac{dv}{dt}=bt
\\
\therefore v=\int{\sqrt{\left( bt \right)}dt}=\frac{bt^2}{2}+c
\end{align*}
Initially at $t=0, \, v=v_0$
$\Rightarrow c=v_0$
Hence,
$v=\frac{dx}{dt}=\frac{bt^2}{2}+v_0$
Or,
\begin{align*}
x&=\int{\left( \frac{bt^2}{2}+v_0 \right)}dt
\\
&=\frac{bt^3}{6}+v_0t+C'
\end{align*}
At $t=0,\, x=0$
$\therefore$ $C'=0$
Therefore,
$x=v_0t+\frac{1}{6}bt^3$
Question 1 :- Give an example which shows that a positive acceleration can be associated with a slowing down object.
Question 2 :- is the acceleration of a car greater than when accelerator is pushed to the floor or when break pedal is pushed hard.
Question 3 :- suppose the acceleration of a body varies with time. Then what does area under its acceleration – time graph for any time interval represent.
Question 4 :- The ϑ –t graphs of two objects make angle of and with the time axis. Find the ratio of their acceleration.
Question 5 :- is it possible that your cycle has northward velocity but southward acceleration? If yes, how?