

On opening of valve air at pressure P and total volume of air in both the vessels would be 2V. since number of moles of air in both the vessels is equal so. from ideal gas equation we have
for vessel
(1) PV = μ1RT
(2) 2PV = μ2RT/2
after air is mixed up
2P'V =(μ1+ μ2)RT'
Where P' and T' are final pressure and temperature
Again considering two portions of air as single system. Since the system is a thermally insulated vessel containing air so total heat transfer of combined system is zero i.e. Q = 0
Since no mechanical work is done on the system or done by the system => work done W = 0.
As no heat transferred takes place and no net amount of work has been done so there would be no change in internal energy of the combined system and would equal sum of internal energies of two partitions of air.
Ui = U1+ U2
= μ1RT/(γ-1)+μ1R(T/2)/(γ-1)
and final internal energy
Uf = (μ1+ μ2)RT'/(γ -1)
μ1RT/(γ-1) + μ1R(T/2)/(γ-1) = (μ1+ μ2)RT'/(γ -1)
or T' = (μ1+ μ2) = (2μ1+ μ2)T/2
μ1= PV/RT
μ2= 4PV/RT
=> T'[(PV/RT + 4PV/RT) = 1/2(2PV/RT + 4PV/RT)T
5T' = (1/2) 6T
T' = (3/5 )T
P' = (μ1+ μ2)RT'/2V
=5PV/RT x R/2V x 3/5 T
P' = (3/2)P
So final answer is
T' = (3/5 )T
P' = (3/2)P
Since the process is cyclic so change in internal energy would be zero.
From first law of thermodynamics
W = Q
now work done is equal to area under this cycle which is
$W = \pi R^2$
$= \pi (100 cc)(100 kpa)$
$=3.14 \times 10$
$= 31.4$ J
=> heat absorbed by system during cyclic process is 31.4 J.
(a) Work done in forming 1 Kg of steam at 120 °C is
$W = P dV$
= 2 x 105 x 0.824m3 x 1.01
= 1.67 x 105 J.
(b) Increase in internal energy is
$\Delta U = Q - W$
where Q = MLv
where Lv is latent heat of vaporization of water
Q = 1 kg x 2256 J / gm
= 1000 x 2256 J / gm
= 2.256 x 106 J
now $ \Delta U = 2.256 \times 10^6 - .167 \times 10^6$ J
$= 2.092 \times 10^6 $ J
(a) Change in internal energy ΔU remains same for all paths as it depends on initial and final points i and f not on the paths through which system is taken from initial point to final point
(b) Work done by gas along these paths is ranked as 1, 2, 3, 4 i.e., work done is greatest along path 1 because area under path 1 is greatest and area covered under path 4 is lowest
(c) from first law of thermodynamic
ΔU = Q - W
or Q = ΔU + W
from this magnitude of energy transferred as heat is greatest along path 1 and then subsequently on path 2,3 and 4.
(a) PV diagram of process is
(b) since the gas is expending at constant pressure so when its volume gets tripled its temperature also gets tripled.
for gas expending at constant pressure heat dQ flowing into gas is
dQ= nCpdT
Integrating both sides with limits of T going from T1 and T2
∫dQ=∫nCpdT
Q=nCp T2 - T1)
given that
Cp = 20.78 J/mol-k
n = 2 mol.
T1 = 27°C = 300 k
T2 = 3 x 300 = 900 k
= 2 x 20.78 x (900 - 300)
= 2.5 x 104 J
(c) Total change in internal energy of helium is zero as initial and final temperature of the process is same
(d) for total work done by helium calculate work done by gas in isobaric process AB and also work done by gas during adiabatic process BC.
now from ideal gas equation
PV = μRT
Initial pressure
P = μRT/V = (2 x 8.314 x 300)/(20 x 10-3)
= 2.49 x 105 N/m2
At point B
PB = PA = 2.49 x 105 N/m2
volume VB = 3VA = 60 x 10-3 m3
and TB = 900 k.
Thus work done by gas during isobaric process AB
= 2.49 x 105 (60 - 20) x 10-3
=9960 J.
Work done by gas during adiabatic process BC
= (μR/(1 - γ))(TB - TC)
= [2 x 8.314/1- (5/3)] [30-900]
;= 14940
Therefore net work done by gas
W = WAB + WBC
= 9960 J + 14940 J
= 2.49 x 104 J
(e) from adiabatic equation
TVγ-1 = Constant
TBVBγ-1 = TCVCγ-1
or, (VC / VB)γ-1 = TB/TC = 900 / 300 = 3
VC/VB = (3) 1/γ-1 = (3) 1.5
= 5.196
VC = 5.196 x VB
= 5.196 x 60 x 10-3m3
= 311.7 x 10-3m3
final pressure
PC = μRTC / VC
= 2 x 8.3 x 300 / 311.7 x 10-3
= .159 x 105 N/m3
(a) Work done when system undergoes isobaric process is
W = PdV
from ideal gas equation
PV = μRT
here μ = 1
=> PdV = RμT
or W = RΔT
, = 8.314 x 80
= .665 KJ
(b) from first law of thermodynamics
ΔU = Q- W = Q- RΔT
given that Q= 3.2 KJ
ΔU = 3.2 KJ - .665 KJ
= 2.536 KJ
(C) Again the know that
ΔU = μCvΔT
= RΔT / γ-1
γ-1 = RΔT / ΔU
or γ= (RΔTT / ΔU) +1
= (.665 KJ x 8.314/ 2.535KJ) +1
= 1.26
(a) Change in internal energy ΔU = 0 for the whole process
(b) during Isochoric process work done would be equal to zero = W1 = 0
now work done during isobaric process is
W = PΔV
= μRΔT
At the end of Isochoric process temperature of the gas can be calculated as follows
In the beginning of Isochoric process ideal gas equation is
PV=nRT0 (1)
During Isochoric process volume remains constant and at the end of the process pressure becomes P/2 and temperature becomes T'
Thus at the end of process ideal gas equation becomes
PV=nRT' (2)
From 1 and 2 T'=T0/2
Now since temperature is increasing from T0/2 to T0
W=μR(T0 -(T0 /2))
(c) total heat absorbed is given by ΔU = Q-W
from first law of thermodynamics
Q= W
total heat absorbed
Q= μRT0 (1-1/n)
= 2 x 8.314 x 300 x (1-1 / 2)
= 2494.25
= 2.5 KJ
(a) As given in the question
$Q= -\Delta U$
so $dQ= -dU= - \mu C_v dT$
$= \frac {\mu R}{\gamma -1} dT$
now molar heat capacity
$C = (\frac {1}{\mu}) (\frac {dQ}{dT})$
$= - \frac {R }{ \gamma -1}$
(b) From first law of thermodynamics we have
$dQ= dU + dW$
but here : dQ= -dU
$- dU= dU+ dW$
or $- 2 dU = dW$
or $-2 \mu C_v dT = P dV$
or $(-2\ mu \frac {R }{ \gamma -1} dT = (\frac {\mu RT }{ V}) dV$
$(\frac {dT}{ T}) + (\frac {\gamma -1 }{ 2 V})(\frac {dV}{V})=0$
On integrating me get
$TV^{\frac {\gamma -1}{2}} = constant$
which is the required equation
(c) As found earlier work done
$dW = - 2dU$
or $W = - 2 (U_2 - U_1 )$
$= -2 C_vT_0((\frac {T }{ T_0}) - 1)$
= 2 CV T0 (1 - (T / T0))
Now as we know that
TV(γ-1)/2 = constant = T0V0(γ-1)/2
(T / T0) = (V0 / V) (γ-1)/2 = 1-(1 / η(γ-1)/2)
So, W = 2 Cv T0 (1 - T / T0)
=2 CV T0 [1 - 1 / (η)(γ-1)/2]
= (2RT0 / γ-1) [1 - 1 / (η)(γ-1)/2]
Given that
P / T = const.
from ideal gas equation
P / T = μR / V = constant
V = μRT / P = constant
Since volume remains constant in this process =>V = 0
or W = pdV = 0
Work done during the process is zero.
Given that number of moles of gas is μ= 2.0 mole and heat rejected Q= 1200 J.
given process is cyclic so dU= 0
from first law of thermodynamic
dQ= dW
during CA volume remains constant
WCA = 0
along AB
T ∝ V
=> T /V = const.
now from ideal gas eqn.
PV = μRT
P=μRT /V=constant
WAB = P(V2 - V1)
= μRT2- μRT1
= 2 x 8.3 x (500 - 300)
= 3320 J
now total work done
W = WAB + WBC
W = 3320 + WBC
from first law of thermodynamics
Q= W
AS heat is being taken of
-Q = W
- 1200 J = 3320 J + WBC or WBC = - 4520 J
(a) W = 0 since vessel has fixed volume and no heat is exchanged between system and surrounding total internal energy of system will remain constant.
(b) Total energy of system before and after the process will remain some now before process internal energy of system is
Ui= 1.5 μ1 RT1 + 1.5 μ2 RT2
and after the process
Uf= 1.5 (μ1 + μ2) RT
where T is the final equilibrium temperature
Now Ui=Uf
1.5 μ1 RT1 + 1.5 μ2 RT2= 1.5 (μ1 + μ2) RT
or T = (μ1T1 + μ2T2) / (μ1 + μ2
) from ideal gas equation
μ= PV / RT
=> μ1 = P1V1 / RT1
=> μ2 =P2V2 / RT2
So
T = (P1 + P2) T1T2 / (P1T2 + P2T1)
or T = (P1 + P2) T1T2 /λ
where λ = P1T2 + P2T1
c) If P1' and P2' are pressures on left and right sides respectively then
P1V1/ RT1 =P1'V1 / RT
=>
P1' = P1T / T1
putting value for T
= P1 (P1 + P2) T1T2 /λ T1
or P1' = T2P1 (P1 + P2) T1T2 /λ
similarly
P2' = P2T / T2
P2' = T1P2 (P1 + P2) T1T2 /λ
a. Change in internal energy = CvΔT=RΔT/(y-1)
b. work done by the gas
given that
P=aT2
Now we know that PV=RT
so, P=a(PV/R)2
PV2=R2/a
PV2=Constant
Now we know that
for PVy=Constant
Work done is given as=RΔT/(1-y)
Similarly for PVn=Constant
Work done =RΔT/(1-n)
Therefore work done in this case
W=RΔT/(1-2)
=-RΔT
c. Molar heat capacity is given by
a. for Vessel A ,walls are adiabatic
so PVγ=constant
P0V0γ= P(3V0)γ
P= P0/3γ
Also
TVγ-1=constant
T= T0/3γ-1
For vessel B ,wall are diathermic, so final temperature is going to be T0 only
So P0V0=P* 3V0
P=P0/3
b. Now when the valve is opened again, final temperature will be again T0
Also
Initially P0V0=nRT0
finally
P*3V0=nRT0
therefore
P=P0/3
a.
Initial State
Initial Pressure = [P0 + (W/A)]
Initial volume = V0
Initial temperature from PV=RT
=[P0 + (W/A)]V0/R
Final state
Pressure remain constant so
Final Pressure = [P0 + (W/A)]
Final volume = 2V0
Final temperature from PV=RT
=2[P0 + (W/A)]V0/R
b. Work done by the gas
= ∫PdV
Since pressure remains constant
=[P0 + (W/A)]V0
c. Change in internal energy is given by
= CVΔT
= [{R/(γ-1)})[P0 + (W/A)]V0/R
= [P0 + (W/A)][V0/(γ-1)]
d Heat supplied
Q= ΔU +W
= [P0 + (W/A)][V0/(γ-1)] + [P0 + (W/A)]V0
=[P0 + (W/A)][V0y/(γ-1)]

a. For sample A
Since Q=0 therefore Adiabatic process
P0V0γ= PA(2V0)γ
PA=P0/2γ
For sample B
Since ΔU=0,therefore Isothermal
So P0V0=PB 2V0
PB=P0/2
So PA : PB = 1 : 2γ-1
b. For sample A
T0V0γ-1=TA(2V0)γ-1
TA = T0/2γ-1
for sample B
TB = T0
So TA : TB = 1 : 2γ-1
c. Work done by the Sample A
For monatomic gas
Cp=5R/2
Cv=3R/2
a Work done by the gas = Area enclosed by the curve ABCDA
=3P0V0
b. Heat absorbed the gas in AB
QAB=Cv(TB-TA)
=3R/2(3P0V0/R -P0V0/R)
=3P0V0
Heat absorbed the gas in BC
QBC=CP(TC-TB)
=5R/2(6P0V0/R - 3P0V0/R)
=15P0V0/2
c. Heat rejected in DA
QDA=CP(TA-TD)
=-5P0V0
Now for the cycle process
QAB+QBC+QCD+QDA=W
So
QCD= -5P0V0/2
d. from diagram and PV=RT
TC=6P0V0/R
TD=3P0V0/R
e. Max temperature will be on the slope CD
Equation of Slope CD as Coordinated system
P=-(2P0/V0)V + 7P0
Now PV=RT
So
RT= -(2P0/V0)V2 + 7P0
For max
dT/dV should be zero
So RdT/dV=-4P0V/V0 +7
V=7V0/4
Tmax= 49P0V0/4R
f. ΔU=0
Net heat=3P0V0
Let m be the mass of the container. Since specific heat varies with temperature, we will have to integrate to total heat lost from container.
dQ=msdT
dQ=m(A+BT)dT
Integrating for the upper and inner limit 300 and 500 respectively
Q= ∫m(A+BT)dT
Q=m[AT +BT2/2]
=-21600m
now heat gained by the ice
Q= heat given to 0° (ice) to 0°(water) + heat required to raise the temperature from o to 27°C
Q=mL + mcΔT
=.1 * 80000 + .1*10-3*27
=10700 cal
Now heat gained =Heat lost
So
21600m=10700
m=.495kg
|
Gas |
No of moles |
Adiabatic coefficient |
|
A |
1 |
1.67 |
|
B |
2 |
1.4 |
a.Let Cp ,Cv and ym are the heat capacities and adiabatic coefficient of the mixture.
then ym=Cp/Cv
Now Cp=nACpA+nBCpB/nA+nB
Also Cv=nACvA+nBCvB/nA+nB
So ym=nACpA+nBCpB/nACvA+nBCvB
Substituting the values
ym =1*5/2R + 2*7/2R/1*3/2R +2*5/2R
=19/13
Work done by the mixture is given as
=nRΔT/y-1
=39RΔT/6
b. Molar mass of the mixture will be =m1+2m2
Speed of sound=√yRT/M
=&radic 19RT0/13(m1+2m2)
n=1
γ=1.4
1. Molar heat capacity of the gas in the Process X->Y (Adiabatic)=0 as Heat is zero
Molar heat capacity of the gas in the Process Y->Z (pressure constant)=Cp =7/2R
Molar heat capacity of the gas in the Process Z->A (Adiabatic)=0 as Heat is zero
Molar heat capacity of the gas in the Process A->X (Volume constant)=Cv =5/2R
2. VX/VY=16
For adiabatic compression X->Y
TXVXγ-1=TYVYγ-1
TX= TY(VY/VX)γ-1
=909 (1/16).4
=300K
Now Y->Z ,According to Charles law
VZ/TZ=VY/TY
So TZ= 909*2=1818 K
Heat absorbed in Y->Z>
=nCp(TZ-TY)
=.3182R
WXY= -nR(TY-TX)/γ-1
=-5R/2* 609
WYZ=nR(TZ-TY)
=909R
WZA= -nR(TZ-TA)/γ-1
Now we know that VX/VY=16 and VZ/VY=2
as VX=VA
So VZ/VA=1/8
Now for Z->A Adiabatic expansion
TZVZγ-1=TAVAγ-1
TA=TZ(VZ/VA)γ-1
=791K
So
WZA =5R/2 * 1027
Also WAX=0 as volume constant
Then
WNET=909R + 5R/2(1027-609)
=1954R
Now For adiabatic compression X->Y
PXVXγ=PYVYγ
PY/PX= 161.4
Similarly
Now for Z->A Adiabatic expansion
PZVZγ=PZVZγ
PZ/PA= 81.4
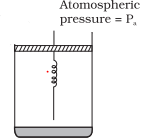
(a): It is considered that piston is mass less and piston is balanced by atmospheric pressure ($P_a$). So the initial pressure of system inside the cylinder = $P_a$.
(b) On supply heat Q. Volume of gas increases from $V_0$ to $V_1$ and spring stretched also.
$\Delta V = V_1 - V_0$
If displacement of piston is x then volume increase in cylinder
$\Delta V= \text {Area of base} \times {height} = A \times x$
$A \times x = V_1 - V_0 $
$x = \frac {V_1 -V_0}{A}$
$x=V_1 -V_0$
As A=1
Force exerted by spring $F_S = K(V_1 -V_0 )$
So final total pressure on gas $P_f = P_a + K(V_1 - V_0)$
(c) By Ist law of thermodynamics
$dQ = dU + dW$
$dU = C_V(T - T_0)$
$T = \frac {PV}{R} = \frac {[P_a + K(V_1 - V_0)]V_1}{R}$
Now
W.D. by gas = p. dV + increase in PE of spring
$dW = P_a(V_1 -V_0) + \frac {1}{2} K(V_1 -V_0)^2$
Now $dQ = dU + dW$
So,
$Q= C_V(T - T_0) + P_a(V_1 -V_0) + \frac {1}{2} K(V_1 -V_0)^2$
Where $T= \frac {[P_a + K(V_1 - V_0)]V_1}{R}$
It is required relation.