In this page we have P-V Diagram Problems and Solutions on heat and thermodynamics for JEE and Competitive examinations . Hope you like them and do not forget to like , social share
and comment at the end of the page.
Question 1
A cyclic Process ABCA as shown in below V-T diagram is performed with a constant mass of ideal gas.Show the process in the P-V digram Solution
A straight line between A to B on V-T diagram indicates $V \alpha T$.So Pressure is constant.
Volume is constant from B-C .Now since temperature is decreasing, Pressure must decrease
Temperature is constant,So Isothermal process
Question 2
A cycle followed by an engine (made of one mole of perfect gas in a cylinder with a piston) as shown above
A to B : volume constant
B to C : adiabatic
C to D : volume constant
D to A : adiabatic
(a) In which part of the cycle heat is supplied to the engine from outside?
(b) In which part of the cycle heat is being given to the surrounding by the engine? Solution
Heat Supplied to the engine in Process A to B
heat is being given to the surrounding in Process C to D
Question 3: The internal energy of an ideal gas depends on
(a) Temperature
(b) Pressure
(c) Volume
(d) None of these Solution
It depend on temperature only
Question 4
The below are P-V diagrams for cyclic processes for a gas.Which of the below processes heat is absorbed by the gas? Solution
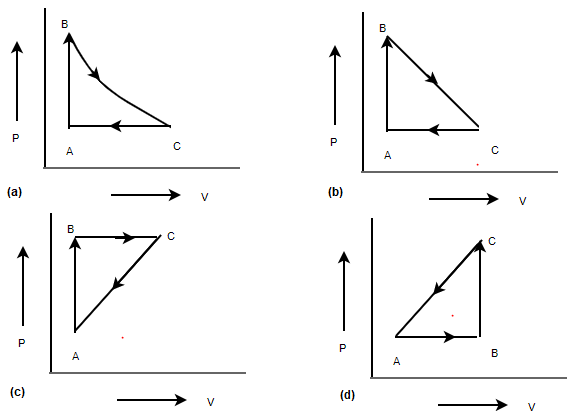
In a cyclic Process,heat is absorbed by a gas when the work done by it is positive. i.e Work done in the P-V diagram should be positive.
Now Work is done by the gas in a cyclic process in the P-V diagram ,if the process is clockwise and it is negative if it is anticlockwise.Here P is on Y-axis and V is on X-axis
Now if P is on x axis and V is on Y-axis, the work done is positive , it cycle moves anticlockwise and negative ,it is clockwise
Keeping the above in mind, option (a) and (c) are correct
Question 5
An ideal gas is taken through a cyclic thermodynamics process through four steps.
The amount of heat involved in the steps are Q1 = 5960 J,Q2 = - 5600 J,Q3= -3000 J,Q4 = -3600 J
respectively. The corresponding quantities of Internal energy changes are ΔU1 = 3.760 J ,ΔU2 = - 4800 J,ΔU3 = -1800 J,ΔU4 = ?
find the value ΔU4 & net work done
(a) 2930 J, 960 J
(b) 2830 J, 900 J
(c) 2930 J, -960 J
(d) -2930 J, 960 J Solution
Since in cycle process total internal change is zero .
ΔU1 + ΔU2 + ΔU3 + ΔU4 = 0
3670 - 4800 - 1800 + ΔU4 = 0
ΔU4 = 2930 J
Now in Cycle
ΔW = ΔQ
= 5960 - 5600 - 3000 + 3600 = 960 J.
Hence answer is a
Question 6
4 moles of an ideal gas undergoes an isothermal expansion at temperature T during which the volume becomes $\eta$ times.
W -> Work done by the gas
$\Delta U$ -> Change in internal energy
(a) $W=-4RT ln \eta$
$\Delta U =0$
(b) $W=-RT ln \eta$
$\Delta U =\frac {6RT}{5}$
(c) $W=RT ln \eta$
$\Delta U =\frac {6RT}{5}$
(d) $W=4RT ln \eta$
$\Delta U =0$ Solution
As temperature is constant ,internal energy will remain constant
$W=nRT ln \frac {V_2}{V_1}$
So ans is d
Question 7
A cyclic Process is shown in the given below p-T digram. Which of the following curves shows the same process in p-V diagram Solution
(a)
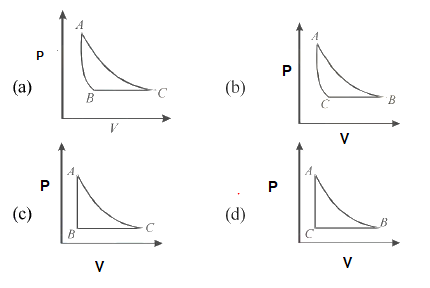
This can be easily solved with ideal Gas equation
$PV=nRT$
At constant T, P is inversely proportional to V .An isotherm Curve
At constant Pressure, Volume is directly proportional to T. An straight line
At constant volume, Pressure is directly proportional to T. An straight line
Question 8
A cyclic Process is shown in the given below p-T digram. Which of the following curves shows the same process in V-T diagram Solution
(a)
Question 9
A cyclic Process is shown in the given below p-T digram.Here AC is an adiabatic Process Which of the following curves shows the same process in P-V diagram Solution
(b)
Question 10
n moles of an ideal gas undergoes an process A to B as shown in the below figure. The maximum temperature of the gas during the process is
(a) $\frac {9P_0V_0}{2nR}$
(b) $\frac {9P_0V_0}{nR}$
(c) $\frac {9P_0V_0}{4nR}$
(d) $\frac {3P_0V_0}{2nR}$ Solution
Equation of line will be
$P =mV +c$
Now putting boundary condition
$2P_0 =mV_0 +c$ -(1)
$P_0 =m(2V_0) +c$ -(2)
Solving (1) and (2)
$m= -\frac {P_0}{V_0}$
$c=3P_0$
So equation is
$P =(-\frac {P_0}{V_0}) V + 3P_0$ --(3)
or
$PV_0 = -P_0 V + 3P_0V_0$
Now PV=nRT or $P =\frac {nRT}{V}$
Therefore,
$\frac {nRT}{V} V_0=-P_0 V + 3P_0V_0$
$nRTV_0 = -P_0v^2 + 3P_0V_0 V$
Differentiating with respect to V
$nRV_0 \frac {dT}{dV} = -2P_0V + 3P_0V_0$
Now T will be maximum ,when
$\frac {dT}{dV}= 0$
Therefore $V= \frac {3V_0}{2}$
From (3) , $P= \frac {3P_0}{2}$
Therefore from $PV=nRT$
$T_{max}=\frac {9P_0V_0}{4nR}$
Question 11
A system goes from state A to B via path I and II
$\Delta U_1$ -> Change in internal energy in Path I
$\Delta U_2$ -> Change in internal energy in Path II
Which of the following is true?
(a) $\Delta U_1 > \Delta U_2$
(b) $\Delta U_1 < \Delta U_2$
(c) $\Delta U_1 = \Delta U_2$
(d) Relation between $\Delta U_1$ and $\Delta U_2$ cannot be determined Solution
(c) as internal energy is a state variable
Question 12
Match the Column I to Column II Solution
JK -> Here Volume is constant so,$\Delta W=0$, Hence $\Delta Q= \Delta U$ , Now since $p \alpha T$, Pressure has decrease,So temperature will decrease .So both $\Delta Q < 0$ and $\Delta U < 0$ . So option (s) and (u)
KL -> Here pressure is constant and volume is increasing , $\Delta W > 0$. Also as Volume is increasing ,temp will increase, So $\Delta U > 0$, Therefore $\Delta Q > 0$. So option (p),(q) and (r)
LM -> Here Volume is constant so,$\Delta W=0$, Hence $\Delta Q= \Delta U$ , Now since $p \alpha T$, Pressure has increase,So temperature will increase .So both $\Delta Q > 0$ and $\Delta U > 0$ . So option (q) and (r)
MJ -> Here since Volume decrease, $\Delta W < 0$, Also we can see that final temperature decrease, $\Delta U < 0$, hence $\Delta Q < 0$.So option (s) ,(t) and (u)
Question 13 An ideal gas under goes an process show in P-V diagram.
Which of the diagram represent it on V-T diagram Solution
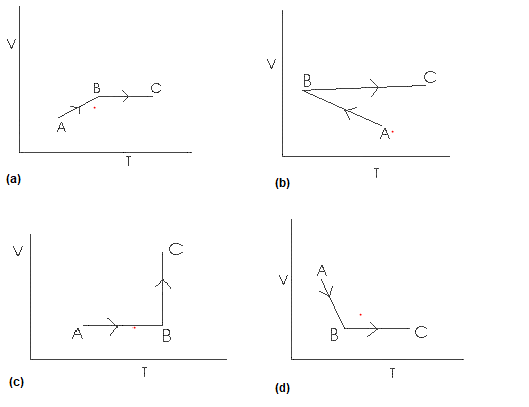
In A to B process
P =constant
so PV = nRT
V is proportional to T
so volume should increase with temp.
In B to C
V = Constant
PV = nRT
P is proportional to T
So pressure increase, temperature increases
link to this page by copying the following text Also Read
