Latest Articles

Second law of thermodynamics

First law of thermodynamics states the equivalence of heat and energy.
It does not state anything about the limitation in the conversion of heat into work or about the condition necessary for such conversion.
Second law of thermodynamics is generalization of certain experience and observation and is concerned with the direction in which energy flow takes place.
This law can be stated in number of ways. Although differently said, they are essentially equivalent.
(i)Kelvin Plank Statement :
"It is impossible to construct a device which, operating in a cycle, has a sole effect of extracting heat from a reservoir and performing an equivalent amount of work".
(ii)Clausius Statement :
"It is impossible for a self acting machine, unaided by external agency, to transfer heat from a colder body to a hotter body".
It can be proved that these two statements of second law are completely equivalent and violation of Kelvin Plank statement leads to violation of Clausius statement and vice-versa.

The Second Law of Thermodynamics gives a fundamental limitation to the efficiency of a heat engine and the co-efficient of performance of a refrigerator.

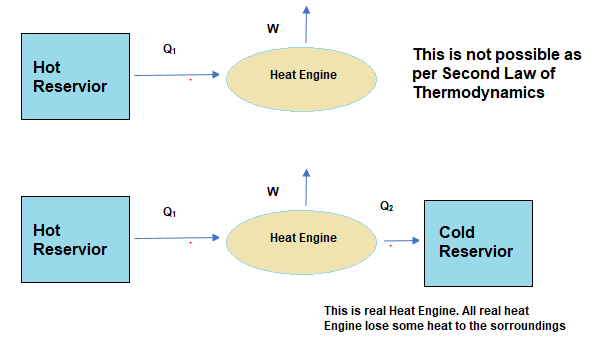
Second laws states that the efficiency of a heat engine can never be unity.According to Heat Engine efficiency equation this implies that heat released to the cold reservoir can never be made zero. Second law of thermodynamics working with Heat engine

Second law of thermodynamics working with Heat engine

The Kelvin and Plank Statement denies the possibility of a perfect heat engine

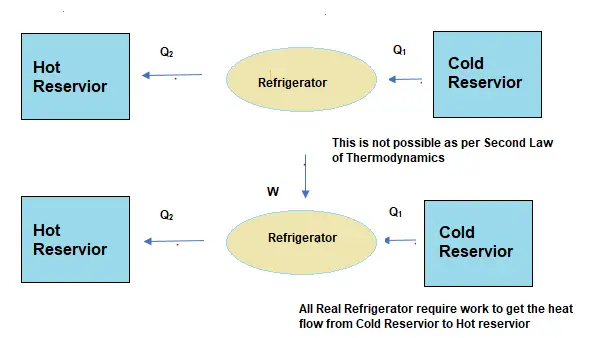
For a refrigerator, the Second Law says that the co-efficient of performance can never be infinite. According to co-efficient of performance equation, this implies that external work (W) can never be zero. Second law of thermodynamics working with Heat pump

Second law of thermodynamics working with Heat pump

Clausius Statement denies the possibility of a perfect refrigerator or heat pump

Solved Examples

Question 1
Consider a cycle followed by an engine in below figure
1 to 2 is isothermal
2 to 3 is adiabatic
3 to 1 is adiabatic
alt=

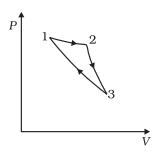
Such a process does not exist because
(a) heat is completely converted to mechanical energy in such a process, which is not possible.
(b) mechanical energy is completely converted to heat in this process,which is not possible.
(c) curves representing two adiabatic processes don't intersect.
(d) curves representing an adiabatic process and an isothermal process don't intersect
Solution
Answer (a) and (c)
Here in this cycle ,we can observe that heat is supplied to the cycle in Isothermal process and there is no heat released in other two process as they are adiabatic Process. So the engine has converted all heat supplied to mechanical work which is not possible as per second law of thermodynamics
We can also prove in the below manner
For Isothermal Process
$\Delta Q_1 =\Delta W_1$
For 2 to 3 adiabatic Process
$\Delta Q_2 =0$ since no heat transfer
$\Delta U_1 =- \Delta W_2$
For 3 to 1 adiabatic Process
$\Delta Q_3 =0$
$\Delta U_2 =- \Delta W_3$
So we can say for whole cycle
$\Delta Q_1 + \Delta Q_2 + \Delta Q_3 =\Delta W_1$
So all the heat supplied is converted into mechanical work which is not possible as per second law of thermodynamics
So (a) is correct
Now (c) is also correct i.e two adiabatic Process cannot intersect as then a cycle can be formed which will violate the second law of thermodynamics

Also Read