Thermodynamics Questions for Class 11, NEET and JEE

On opening of valve air at pressure P and total volume of air in both the vessels would be 2V. since number of moles of air in both the vessels is equal so. from ideal gas equation we have
for vessel
(1) PV = μ₁RT
(2) 2PV = μ₂RT/2
after air is mixed up
2P^'V =(μ₁+ μ₂)RT^'
Where P^' and T^' are final pressure and temperature
Again considering two portions of air as single system. Since the system is a thermally insulated vessel containing air so total heat transfer of combined system is zero i.e. Q = 0
Since no mechanical work is done on the system or done by the system => work done W = 0.
As no heat transferred takes place and no net amount of work has been done so there would be no change in internal energy of the combined system and would equal sum of internal energies of two partitions of air.
U_i = U₁+ U₂
= μ₁RT/(γ-1)+μ₁R(T/2)/(γ-1)
and final internal energy
U_f = (μ₁+ μ₂)RT^'/(γ -1)
μ₁RT/(γ-1) + μ₁R(T/2)/(γ-1) = (μ₁+ μ₂)RT^'/(γ -1)
or T^' = (μ₁+ μ₂) = (2μ₁+ μ₂)T/2
μ₁= PV/RT
μ₂= 4PV/RT
=> T^'[(PV/RT + 4PV/RT) = 1/2(2PV/RT + 4PV/RT)T
5T^' = (1/2) 6T
T^' = (3/5 )T
P^' = (μ₁+ μ₂)RT^'/2V
=5PV/RT x R/2V x 3/5 T
P^' = (3/2)P

So final answer is
T^' = (3/5 )T
P^' = (3/2)P

 

Since the process is cyclic so change in internal energy would be zero.
From first law of thermodynamics
W = Q
now work done is equal to area under this cycle which is
$W = \pi R^2$
$= \pi (100 cc)(100 kpa)$
$=3.14 \times 10$
$= 31.4$ J
=> heat absorbed by system during cyclic process is 31.4 J.

(a) Work done in forming 1 Kg of steam at 120 °C is
$W = P dV$
= 2 x 10⁵ x 0.824m³ x 1.01
= 1.67 x 10⁵ J.
(b) Increase in internal energy is
$\Delta U = Q - W$
where Q = ML_v
where L_v is latent heat of vaporization of water
Q = 1 kg x 2256 J / gm
= 1000 x 2256 J / gm
= 2.256 x 10⁶ J
now $ \Delta U = 2.256 \times 10^6 - .167 \times 10^6$ J
$= 2.092 \times 10^6 $ J


 

(a) Change in internal energy ΔU remains same for all paths as it depends on initial and final points i and f not on the paths through which system is taken from initial point to final point
(b) Work done by gas along these paths is ranked as 1, 2, 3, 4 i.e., work done is greatest along path 1 because area under path 1 is greatest and area covered under path 4 is lowest
(c) from first law of thermodynamic
ΔU = Q - W
or Q = ΔU + W
from this magnitude of energy transferred as heat is greatest along path 1 and then subsequently on path 2,3 and 4.

 

(a) PV diagram of process is

(b) since the gas is expending at constant pressure so when its volume gets tripled its temperature also gets tripled.
for gas expending at constant pressure heat dQ flowing into gas is
dQ= nC_pdT
Integrating both sides with limits of T going from T₁ and T₂
∫dQ=∫nC_pdT
Q=nC_p T₂ - T₁)
given that
C_p = 20.78 J/mol-k
n = 2 mol.
T₁ = 27°C = 300 k
T₂ = 3 x 300 = 900 k
= 2 x 20.78 x (900 - 300)
= 2.5 x 10⁴ J
(c) Total change in internal energy of helium is zero as initial and final temperature of the process is same
(d) for total work done by helium calculate work done by gas in isobaric process AB and also work done by gas during adiabatic process BC.
now from ideal gas equation
PV = μRT
Initial pressure
P = μRT/V = (2 x 8.314 x 300)/(20 x 10^-3)
= 2.49 x 10⁵ N/m²
At point B
P_B = P_A = 2.49 x 10⁵ N/m²
volume V_B = 3V_A = 60 x 10^-3 m³
and T_B = 900 k.
Thus work done by gas during isobaric process AB
= 2.49 x 10⁵ (60 - 20) x 10^-3
=9960 J.
Work done by gas during adiabatic process BC
= (μR/(1 - γ))(T_B - T_C)
= [2 x 8.314/1- (5/3)] [30-900]
;= 14940
Therefore net work done by gas
W = W_AB + W_BC
= 9960 J + 14940 J
= 2.49 x 10⁴ J
(e) from adiabatic equation
TV^γ-1 = Constant
T_BV_B^γ-1 = T_CV_C^γ-1
or, (V_C / V_B)^γ-1 = T_B/T_C = 900 / 300 = 3
V_C/V_B = (3) ^1/γ-1 = (3) ^1.5
= 5.196
V_C = 5.196 x V_B
= 5.196 x 60 x 10^-3m³
= 311.7 x 10^-3m³
final pressure
P_C = μRT_C / V_C
= 2 x 8.3 x 300 / 311.7 x 10^-3
= .159 x 10⁵ N/m³
 

(a) Work done when system undergoes isobaric process is
W = PdV
from ideal gas equation
PV = μRT
here μ = 1
=> PdV = RμT
or W = RΔT
, = 8.314 x 80
= .665 KJ
(b) from first law of thermodynamics
ΔU = Q- W = Q- RΔT
given that Q= 3.2 KJ
ΔU = 3.2 KJ - .665 KJ
= 2.536 KJ
(C) Again the know that
ΔU = μC_vΔT
= RΔT / γ-1
γ-1 = RΔT / ΔU
or γ= (RΔTT / ΔU) +1
= (.665 KJ x 8.314/ 2.535KJ) +1
= 1.26

 

(a) Change in internal energy ΔU = 0 for the whole process
(b) during Isochoric process work done would be equal to zero = W₁ = 0
now work done during isobaric process is
W = PΔV
= μRΔT
At the end of Isochoric process temperature of the gas can be calculated as follows
In the beginning of Isochoric process ideal gas equation is
PV=nRT₀ (1)
During Isochoric process volume remains constant and at the end of the process pressure becomes P/2 and temperature becomes T'
Thus at the end of process ideal gas equation becomes
PV=nRT' (2)
From 1 and 2 T'=T₀/2
Now since temperature is increasing from T₀/2 to T₀
W=μR(T₀ -(T₀ /2))
(c) total heat absorbed is given by ΔU = Q-W
from first law of thermodynamics
Q= W
total heat absorbed
Q= μRT₀ (1-1/n)
= 2 x 8.314 x 300 x (1-1 / 2)
= 2494.25
= 2.5 KJ

 

(a) As given in the question
$Q= -\Delta U$
so $dQ= -dU= - \mu C_v dT$
$= \frac {\mu R}{\gamma -1} dT$
now molar heat capacity
$C = (\frac {1}{\mu}) (\frac {dQ}{dT})$
$= - \frac {R }{ \gamma -1}$
(b) From first law of thermodynamics we have
$dQ= dU + dW$
but here : dQ= -dU
$- dU= dU+ dW$
or $- 2 dU = dW$
or $-2 \mu C_v dT = P dV$
or $(-2\ mu \frac {R }{ \gamma -1} dT = (\frac {\mu RT }{ V}) dV$
$(\frac {dT}{ T}) + (\frac {\gamma -1 }{ 2 V})(\frac {dV}{V})=0$
On integrating me get
$TV^{\frac {\gamma -1}{2}} = constant$
which is the required equation
(c) As found earlier work done
$dW = - 2dU$
or $W = - 2 (U_2 - U_1 )$
$= -2 C_vT_0((\frac {T }{ T_0}) - 1)$
= 2 C_V T₀ (1 - (T / T₀))
Now as we know that
TV^(γ-1)/2 = constant = T₀V₀^(γ-1)/2
(T / T₀) = (V₀ / V) ^(γ-1)/2 = 1-(1 / η^(γ-1)/2)
So, W = 2 Cv T₀ (1 - T / T₀)
=2 C_V T₀ [1 - 1 / (η)^(γ-1)/2]
= (2RT₀ / γ-1) [1 - 1 / (η)^(γ-1)/2]

 

Given that
P / T = const.
from ideal gas equation
P / T = μR / V = constant
V = μRT / P = constant
Since volume remains constant in this process =>V = 0
or W = pdV = 0
Work done during the process is zero.

Given that number of moles of gas is μ= 2.0 mole and heat rejected Q= 1200 J.
given process is cyclic so dU= 0
from first law of thermodynamic
dQ= dW
during CA volume remains constant
W_CA = 0
along AB
T ∝ V
=> T /V = const.
now from ideal gas eqn.
PV = μRT
P=μRT /V=constant
W_AB = P(V₂ - V₁)
= μRT₂- μRT₁
= 2 x 8.3 x (500 - 300)
= 3320 J
now total work done
W = W_AB + W_BC
W = 3320 + W_BC
from first law of thermodynamics
Q= W
AS heat is being taken of
-Q = W
- 1200 J = 3320 J + W_BC or W_BC = - 4520 J

 

(a) W = 0 since vessel has fixed volume and no heat is exchanged between system and surrounding total internal energy of system will remain constant.

(b) Total energy of system before and after the process will remain some now before process internal energy of system is
U_i= 1.5 μ₁ RT₁ + 1.5 μ₂ RT₂
and after the process
U_f= 1.5 (μ₁ + μ₂) RT
where T is the final equilibrium temperature
Now U_i=U_f
1.5 μ₁ RT₁ + 1.5 μ₂ RT₂= 1.5 (μ₁ + μ₂) RT
or T = (μ₁T₁ + μ₂T₂) / (μ₁ + μ₂
) from ideal gas equation
μ= PV / RT
=> μ₁ = P₁V₁ / RT₁
=> μ₂ =P₂V₂ / RT₂
So
T = (P₁ + P₂) T₁T₂ / (P₁T₂ + P₂T₁)
or T = (P₁ + P₂) T₁T₂ /λ
where λ = P₁T₂ + P₂T₁

c) If P₁^' and P₂^' are pressures on left and right sides respectively then
P₁V₁/ RT₁ =P₁^'V₁ / RT
=>
P₁^' = P₁T / T₁
putting value for T
= P₁ (P₁ + P₂) T₁T₂ /λ T₁
or P₁^' = T₂P₁ (P₁ + P₂) T₁T₂ /λ
similarly
P₂^' = P₂T / T₂
P₂^' = T₁P₂ (P₁ + P₂) T₁T₂ /λ

a. Change in internal energy = C_vΔT=RΔT/(y-1)
b. work done by the gas
given that
P=aT²
Now we know that PV=RT
so, P=a(PV/R)²
PV²=R²/a
PV²=Constant
Now we know that
for PV^y=Constant
Work done is given as=RΔT/(1-y)
Similarly for PVⁿ=Constant
Work done =RΔT/(1-n)
Therefore work done in this case
W=RΔT/(1-2)
=-RΔT

c. Molar heat capacity is given by

a. for Vessel A ,walls are adiabatic
so PV^γ=constant

P₀V₀^γ= P(3V₀)^γ
P= P₀/3^γ

Also
TV^γ-1=constant

T= T₀/3^γ-1

For vessel B ,wall are diathermic, so final temperature is going to be T₀ only

So P₀V₀=P* 3V₀
P=P₀/3

b. Now when the valve is opened again, final temperature will be again T₀

Also
Initially P₀V₀=nRT₀
finally
P*3V₀=nRT₀

therefore
P=P₀/3

 

a.
Initial State
Initial Pressure = [P₀ + (W/A)]
Initial volume = V₀
Initial temperature from PV=RT
=[P₀ + (W/A)]V₀/R
Final state
Pressure remain constant so

Final Pressure = [P₀ + (W/A)]
Final volume = 2V₀
Final temperature from PV=RT
=2[P₀ + (W/A)]V₀/R

b. Work done by the gas
= ∫PdV

Since pressure remains constant
=[P₀ + (W/A)]V₀

c. Change in internal energy is given by

= C_VΔT
= [{R/(γ-1)})[P₀ + (W/A)]V₀/R
= [P₀ + (W/A)][V₀/(γ-1)]


d Heat supplied
Q= ΔU +W
= [P₀ + (W/A)][V₀/(γ-1)] + [P₀ + (W/A)]V₀
=[P₀ + (W/A)][V₀y/(γ-1)]

 

a. For sample A
Since Q=0 therefore Adiabatic process
P₀V₀^γ= P_A(2V₀)^γ
P_A=P₀/2^γ
For sample B
Since ΔU=0,therefore Isothermal
So P₀V₀=P_B 2V₀
P_B=P₀/2

So P_A : P_B = 1 : 2^γ-1

b. For sample A
T₀V₀^γ-1=T_A(2V₀)^γ-1
T_A = T₀/2^γ-1

for sample B
T_B = T₀

So T_A : T_B = 1 : 2^γ-1

c. Work done by the Sample A

For monatomic gas
C_p=5R/2
C_v=3R/2

a Work done by the gas = Area enclosed by the curve ABCDA
=3P₀V₀

b. Heat absorbed the gas in AB
Q_AB=C_v(T_B-T_A)
=3R/2(3P₀V₀/R -P₀V₀/R)
=3P₀V₀
Heat absorbed the gas in BC
Q_BC=C_P(T_C-T_B)
=5R/2(6P₀V₀/R - 3P₀V₀/R)
=15P₀V₀/2

c. Heat rejected in DA
Q_DA=C_P(T_A-T_D)
=-5P₀V₀

Now for the cycle process
Q_AB+Q_BC+Q_CD+Q_DA=W
So
Q_CD= -5P₀V₀/2
d. from diagram and PV=RT

T_C=6P₀V₀/R
T_D=3P₀V₀/R

e. Max temperature will be on the slope CD

Equation of Slope CD as Coordinated system
P=-(2P₀/V₀)V + 7P₀
Now PV=RT

So
RT= -(2P₀/V₀)V² + 7P₀

For max
dT/dV should be zero

So RdT/dV=-4P₀V/V₀ +7
V=7V₀/4
T_max= 49P₀V₀/4R

f. ΔU=0
Net heat=3P₀V₀

 

Let m be the mass of the container. Since specific heat varies with temperature, we will have to integrate to total heat lost from container.
dQ=msdT
dQ=m(A+BT)dT
Integrating for the upper and inner limit 300 and 500 respectively
Q= ∫m(A+BT)dT
Q=m[AT +BT²/2]
=-21600m

now heat gained by the ice
Q= heat given to 0° (ice) to 0°(water) + heat required to raise the temperature from o to 27°C
Q=mL + mcΔT
=.1 * 80000 + .1*10^-3*27
=10700 cal
Now heat gained =Heat lost
So
21600m=10700
m=.495kg


 

a.Let C_p ,C_v and y_m are the heat capacities and adiabatic coefficient of the mixture.
then y_m=C_p/C_v

Now C_p=n_AC_pA+n_BC_pB/n_A+n_B
Also C_v=n_AC_vA+n_BC_vB/n_A+n_B

So y_m=n_AC_pA+n_BC_pB/n_AC_vA+n_BC_vB

Substituting the values
y_m =1*5/2R + 2*7/2R/1*3/2R +2*5/2R
=19/13

Work done by the mixture is given as
=nRΔT/y-1
=39RΔT/6
b. Molar mass of the mixture will be =m₁+2m₂

Speed of sound=√yRT/M
=&radic 19RT₀/13(m₁+2m₂)


 

n=1
γ=1.4

1. Molar heat capacity of the gas in the Process X->Y (Adiabatic)=0 as Heat is zero
Molar heat capacity of the gas in the Process Y->Z (pressure constant)=C_p =7/2R
Molar heat capacity of the gas in the Process Z->A (Adiabatic)=0 as Heat is zero
Molar heat capacity of the gas in the Process A->X (Volume constant)=C_v =5/2R
2. V_X/V_Y=16
For adiabatic compression X->Y
T_XV_X^γ-1=T_YV_Y^γ-1
T_X= T_Y(V_Y/V_X)^γ-1
=909 (1/16)^.4
=300K
Now Y->Z ,According to Charles law
V_Z/T_Z=V_Y/T_Y
So T_Z= 909*2=1818 K

Heat absorbed in Y->Z>
=nC_p(T_Z-T_Y)
=.3182R

W_XY= -nR(T_Y-T_X)/γ-1
=-5R/2* 609
W_YZ=nR(T_Z-T_Y)
=909R
W_ZA= -nR(T_Z-T_A)/γ-1

Now we know that V_X/V_Y=16 and V_Z/V_Y=2
as V_X=V_A
So V_Z/V_A=1/8

Now for Z->A Adiabatic expansion

T_ZV_Z^γ-1=T_AV_A^γ-1
T_A=T_Z(V_Z/V_A)^γ-1
=791K

So
W_ZA =5R/2 * 1027

Also W_AX=0 as volume constant

Then
W_NET=909R + 5R/2(1027-609)
=1954R

Now For adiabatic compression X->Y
P_XV_X^γ=P_YV_Y^γ
P_Y/P_X= 16^1.4

Similarly
Now for Z->A Adiabatic expansion

P_ZV_Z^γ=P_ZV_Z^γ
P_Z/P_A= 8^1.4

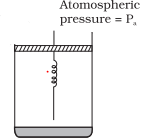
(a): It is considered that piston is mass less and piston is balanced by atmospheric pressure ($P_a$). So the initial pressure of system inside the cylinder = $P_a$.
(b) On supply heat Q. Volume of gas increases from $V_0$ to $V_1$ and spring stretched also.
$\Delta V = V_1 - V_0$
If displacement of piston is x then volume increase in cylinder
$\Delta V= \text {Area of base} \times {height} = A \times x$
$A \times x = V_1 - V_0 $
$x = \frac {V_1 -V_0}{A}$
$x=V_1 -V_0$
As A=1
Force exerted by spring $F_S = K(V_1 -V_0 )$
So final total pressure on gas $P_f = P_a + K(V_1 - V_0)$
(c) By Ist law of thermodynamics
$dQ = dU + dW$
$dU = C_V(T - T_0)$
$T = \frac {PV}{R} = \frac {[P_a + K(V_1 - V_0)]V_1}{R}$
Now
W.D. by gas = p. dV + increase in PE of spring
$dW = P_a(V_1 -V_0) + \frac {1}{2} K(V_1 -V_0)^2$
Now $dQ = dU + dW$
So,
$Q= C_V(T - T_0) + P_a(V_1 -V_0) + \frac {1}{2} K(V_1 -V_0)^2$
Where $T= \frac {[P_a + K(V_1 - V_0)]V_1}{R}$
It is required relation.