Work Done in an Adiabatic Process

Solved Examples

Question 1
A gas ($\gamma =1.4$) of 2m³ Volume and at a pressure of $4 \times 10^5 N/m^2$ is compressed adiabatically to a volume .5 m ³. Find its new pressure. Calculate the work done in the process?
Given $4^{1.4} =6.96$
Solution
For an adiabatic Process
$PV^{\gamma} = K$
Here $P_1=4 \times 10^5 N/m^2$ , $V_1=2m^3$ ,$V_2=.5 m^3$, $P_2=?$
Now $P_1V_1^{\gamma} = P_2V_2^{\gamma}$
or
$P_2 = P_1 (\frac {V_1}{V_2})^{\gamma}= (4 \times 10^5) (\frac {2}{.5})^{\gamma}$
$=2.78 \times 10^6 N/m^2$
Now Work done in an adiabatic process
$W= \frac {1}{1 - \gamma} (P_2V_2 -P_1V_1)$
Substituting all the values , we have
$W=-14.75 \times 10^5$ J

Question 2
Consider a P-V diagram in which the path followed by one mole of perfect gas in a cylindrical container is shown in below figure.
(a) Find the work done when the gas is taken from state 1 to state 2.
(b) What is the ratio of temperature $ \frac {T_1}{T_2}$, if $V_2 = 2V_1$?
(c) Given the internal energy for one mole of gas at temperature T is $ \frac {3}{2} RT$, find the heat supplied to the gas when it is taken from state 1 to 2, with $V_2 = 2V_1$

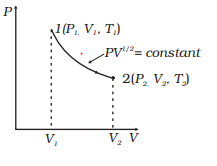Solution
This is clearly an adiabatic Process with $\gamma =\frac {1}{2}$
$PV^{1/2} = Constant$
a. Now work done is given by
$W= \frac {1}{1 - \gamma} (P_2V_2 -P_1V_1)$
or
$W= 2(P_2V_2 -P_1V_1)$
b. Now since $PV=RT$ or $P =\frac {RT}{V}$
So, $PV^{1/2} = Constant$ becomes
$\frac {RT}{V} V^{1/2} = Constant$
$TV^{-1/2} = constant$
Therefore
$T_1 V_1^{-1/2}= T_2 V_2^{-1/2}$
$\frac {T_1}{T_2} = (\frac {V_2}{V_1})^{-1/2}$
or
$\frac {T_1}{T_2}= \frac {1}{\sqrt {2}}$
c. Change in Internal Energy will be given by
$\Delta U = U_2 -U_1 = \frac {3}{2} RT_2 - \frac {3}{2} RT_1= \frac {3}{2}R(T_2 -T_1) = \frac {3}{2}R T_1( \sqrt {2} -1)$
$\Delta W= \frac {nR}{1 - \gamma} (T_1 - T_2) =2R T_1(\sqrt {2} -1)$
Now
$\Delta Q = \Delta U + \Delta W= \frac {3}{2}R T_1( \sqrt {2} -1) + 2R T_1(\sqrt {2} -1)=\frac {7}{2} RT_1(\sqrt {2} -1)$

Question 3
what all is true for a adiabatic process
a. $dQ=0$
b. $dW=-nC_vdT$
c. $TV^{\gamma -1}=constant$
d. all the above
Solution
(d). As all of them are true