

Get a full explanation of the notion of speed and velocity for class 11 physics on this page. These notes can also be used by students studying for competitive exams such as JEE Mains, JEE Advanced, and NEET. We already learned about speed and velocity in the class 9 motion chapter. We will review the concepts of speed and velocity as well as average speed and average velocity.
I have written a separate article on average velocity formula. Do check it out for additional information.
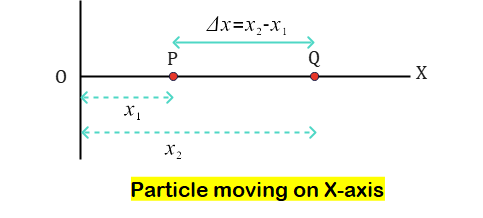
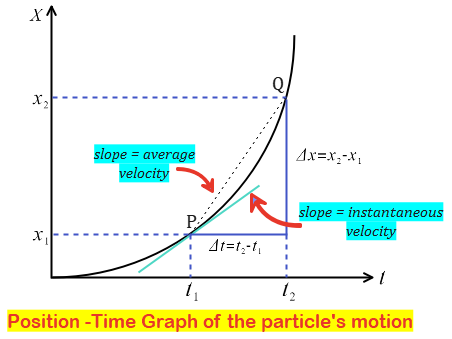
Let us consider an example

The answer is no, average speed is not equal to average velocity. This is because
Average Speed = Total distance/Total time
Average Velocity = Total displacement/Total time
Just like both displacement and distance are different, average speed and average velocity are also different for ex. Motion around a circular track.
The average speed of an object is the ratio of the total distance traveled to the total time taken. The average velocity, on the other hand, is the change in position or displacement $(\Delta x)$ divided by the time intervals $(\Delta t)$ during which the displacement takes place.
Let us now consider some of the solved examples for the concepts Average speed and Average velocity. Questions are important for understanding the concept. Try to understand these solved examples and then try to solve few questions on your own.
Question 1 A car travels first half distance between two places with a speed of 40 Km/hr and the rest half
with a speed of 60 Km/hr. Find the average speed of the car.
Solution Let $x$ be the total distance travelled by the car.
Time taken to travel first half distance ${t_1} = \frac{{x/2}}{{40}} = \frac{x}{{80}}hr$
Time taken to travel rest half distance ${t_2} = \frac{{x/2}}{{60}} = \frac{x}{{120}}hr$
Therefore Average speed = (Total distance)/(Total time) = $\frac{x}{{(x/80) + (x/120)}} = 48Km/hr$
Question 2 A point travelling along a straight line traverse one third the distance with a velocity $v_0$.
The remaining part of the distance was covered with velocity $v_1$ for half the time and with velocity $v_2$ for the other
half of the time. Find the mean velocity of the point averaged over the whole time of motion.
Solution Let $s$ be the total distance. Let $\frac{s}{3}$ be the distance covered in time $t_1$ while the remaining
distance $\frac{2s}{3}$ in time $t_2$ second
$\frac{s}{3} = {v_0}{t_1}$
${t_1} = \frac{s}{{3{v_0}}}$ (1)
and,
$\frac{{2s}}{3} = {v_1}\left( {\frac{{{t_2}}}{2}} \right) + {v_2}\left( {\frac{{{t_2}}}{2}} \right)$
or,
${t_2} = \frac{{4s}}{{3({v_1} + {v_2})}}$ (2)
Average Velocity $ = \frac{s}{{{t_2} + {t_1}}}$
or,
Average Velocity $ = \frac{s}{{\left( {\frac{s}{{3{v_0}}}} \right) + \left( {\frac{{4s}}{{3({v_1} + {v_2})}}} \right)}} = \frac{{3{v_0}({v_1} + {v_2})}}{{{v_1} + {v_2} + 4{v_0}}}$
Question 1 Usually "average speed" means the ratio of total distance covered to total the total time elapsed. However sometimes
the phrase "average speed" can mean magnitude of average velocity. Are the two same?
Solution No, usually they have different meanings, as according to their definitions
Average speed is defined as total distance travelled divided by time taken and Average velocity is defined as change of
displacement divided by the time taken. Now since distance travelled by any particle is either grater then the displacement or it is equal to
the displacement , the velocity would be given as
${v_{av}} \geq |{{\vec v}_{av}}|$
that is usually average speed is greater than the magnitude of average velocity.
For example if a body returns to its starting point after some motion, then as distance travel would be finite while displacement
would be zero. So in this case average speed would be greater then zero but magnitude of average velocity would be equal to zero.
However in case of motion along the straight line without change in direction, magnitude of displacement would be equal to distance
and two definitions would mean the same.
Question 2 A student argues that the mean velocity during an interval of time can also be expressed as
$\vec v = \frac{{{{\vec v}_f} + {{\vec v}_i}}}{2}$ and this should always be equal to $\vec v = \frac{{{{\vec r}_f} - {{\vec r}_i}}}{{{t_2} - {t_1}}}$
. is he right?
Solution: No, he is not right. The correct definition of average velocity is the later one.The first one can be used only when
there is uniform acceleration.