P-V Diagram

P-V Indicator Diagram

• Only two thermodynamic variables are sufficient to describe a system because third variable can be calculated from equation of state of the system.
  
• P-V Indicator Diagram is just a graph between pressure and volume of a system undergoing an operation.
  
• When a system undergoes an expansion from state A (P₁ V₁) to a state B (P₂V₂) its indicator diagram is shown as follows.
  
  
• In case of compression system at state A(P₁ V₁) goes to a state B(P₂V₂) its P-V diagram is as follows.
  
  
  
• Intermediate states of system are represented by points on the curve.
  
• The pressure volume curve for a fixed temperature is called isotherm.
  

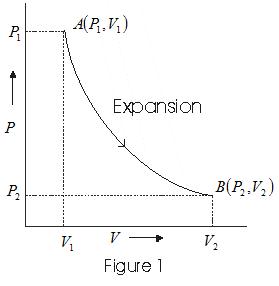
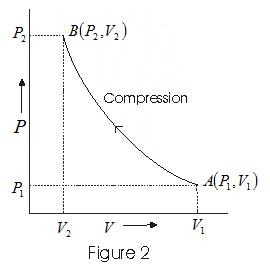
Solved Example of PV diagram

Question 1
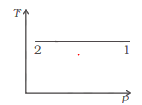
Consider P-V diagram for an ideal gas

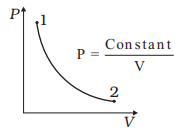
Draw the corresponding T-P diagram
Solution
here
$P= \frac {constant}{V}$
or
$PV= constant$
So it means temperature is constant.So here is the TP diagram


Question 2
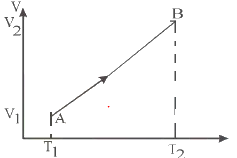
Draw the corresponding P-V diagram for the given T-V diagram

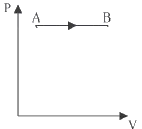
Solution
Since TV diagram is a straight line
T/V =constant
it means Pressure is constant


Question 3
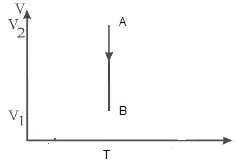
Draw the corresponding P-V diagram for the given T-V diagram

Solution
Since T is constant
PV diagram should be isotherm

• Notes
  • Introduction to Thermodynamics
  • Concept of Heat
  • P-V Diagram
  • Work done by Gas in volume changes
  • Internal Energy
  • First Law of Thermodynamics
  • Specific Heat Capacity of Ideal GAS
  • Thermodynamic Processes
  • Quasi static Processes
  • Isothermal Process
  • Adiabatic Process
  • Isochoric process
  • Isobaric process
  • Cyclic process
  • Work done in Isothermal process
  • Work done in an Adiabatic process
  • Heat Engine and efficiency
  • Principle of a Refrigerator
  • Second law of thermodynamics
  • Reversibility and irreversibility
  • Carnot's Heat Engine
  • Carnot Theorem
  • Solved Examples
• Assignments
  • Thermodynamics Questions
  • Multiple Choice Questions
  • P-V diagram Problems and Solutions
  • Carnot Cycle Problems
• Revision Notes
  • Thermodynamics revision sheet