Concise Class 12 Physics notes covering theory, formulas and practice questions from Electric Charges and Fields.
Electric Charges and Fields Chapter Overview
Electric Charges and Fields is the first chapter of electrostatics in Class 12 Physics. In this chapter, we study the nature of electric charge, laws governing forces between charges, the concept of electric field, electric flux, electric dipole and Gauss's law with applications. This chapter forms the foundation for later topics like electric potential, capacitance and electromagnetic theory.
Syllabus Map
1. Electric Charges
- Concept of electric charges
- Conservation of charge
2. Coulomb’s Law
- Force between two point charges
- Forces between multiple charges
- Superposition principle
- Continuous charge distribution
3. Electric Field
- Definition of electric field
- Electric field due to a point charge
- Representation with electric field lines
- Electric dipole
- Electric field due to a dipole
- Torque on a dipole in a uniform electric field
4. Electric Flux & Gauss’s Theorem
- Concept of electric flux
- Statement of Gauss’s theorem
- Applications of Gauss’s theorem:
- Field due to an infinitely long straight wire
- Field due to a uniformly charged infinite plane sheet
- Field due to a uniformly charged thin spherical shell
- Field inside the shell
- Field outside the shell
Electric Charges and Fields – Concept-wise Short Notes
1. Electric Charge – Properties and Types
Electric charge is a fundamental property of matter responsible for electrical interactions. It is the property associated with matter due to which it produces and experiences electrical and magnetic effects.
Types of Charges:
- Positive charge (proton)
- Negative charge (electron)
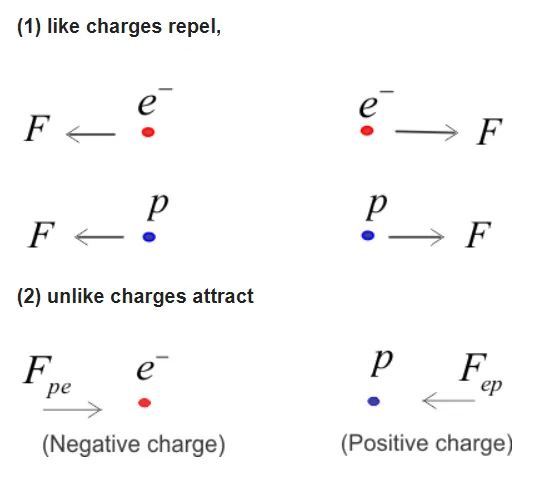
Basic Properties:
1. Additivity of Charges: The total charge of a system is the algebraic sum of all individual charges in the system. If a system contains charges q₁, q₂, q₃, ... qₙ, then the total charge is:
$$Q = q_1 + q_2 + q_3 + ... + q_n$$
2. Conservation of Charge: The total charge of an isolated system remains constant. Charge can neither be created nor destroyed, but can be transferred from one body to another.
3. Quantization of Charge: Electric charge exists only in integral multiples of the elementary charge (charge of an electron, e = 1.6 × 10⁻¹⁹ C). The charge on any body is given by:
$$q = ne$$
where n is an integer (±1, ±2, ±3, ...) and e is the elementary charge.
👉 Detailed theory of electric charge, its properties and methods of charging: Electric Charge, Basic Properties of Electric Charge and Frictional Electricity
2. Electrical and Electrostatic Force
Charged bodies exert force on each other even without physical contact. This force can be:
- Attractive – between unlike charges (positive and negative)
- Repulsive – between like charges (positive-positive or negative-negative)
Key Points:
- Electrostatic force acts along the line joining the two charges
- It is a non-contact force (acts at a distance)
- Electrostatic force is much stronger than gravitational force
- The ratio of electrostatic to gravitational force between two electrons is approximately 10⁴²
👉 Detailed explanation of electrical and electrostatic force with examples: Electrical and Electrostatic Force
3. Coulomb’s Law (Class 12 Physics)
Coulomb’s law gives the magnitude and direction of the electrostatic force between two stationary point charges.
- Force is directly proportional to the product of the charges
- Inversely proportional to the square of the distance between them
- Acts along the line joining the charges
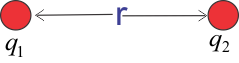
Mathematical Form:
$$F = \frac{1}{4\pi\varepsilon_0}\frac{|q_1 q_2|}{r^2}$$
where $\varepsilon_0 = 8.854 \times 10^{-12}$ C² N⁻¹ m⁻².
Vector Form:
$$ \vec{F}_{12} = \frac{1}{4\pi\varepsilon_0}\frac{q_1 q_2}{r^2}\hat{r}_{12} $$
Here, $\hat{r}_{12}$ is the unit vector directed from charge $q_1$ to $q_2$.
Key Points:
- Applicable only to point charges at rest
- Obeys inverse square law
- Electrostatic force is conservative
👉 Coulomb’s law (scalar and vector form) with solved examples: Coulomb's Law and Coulomb's Law in Vector Form
4. Principle of Superposition of Charges
When multiple charges are present, the net force on any charge is the vector sum of the forces exerted by all other charges, with each force calculated independently using Coulomb's law.
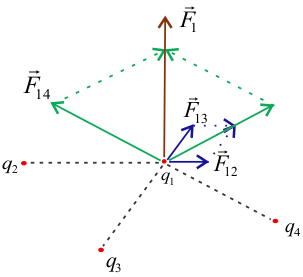
The net force on charge q₀ due to charges q₁, q₂, q₃, ... qₙ is:
$$\vec{F} = \vec{F}_1 + \vec{F}_2 + \vec{F}_3 + ... + \vec{F}_n$$
$$\vec{F} = \frac{q_0}{4\pi\varepsilon_0}\left[\frac{q_1}{r_1^2}\hat{r}_1 + \frac{q_2}{r_2^2}\hat{r}_2 + ... + \frac{q_n}{r_n^2}\hat{r}_n\right]$$
Key Points:
- Forces act independently of each other
- Vector addition is essential
- Applicable to any number of charges
👉 Principle of superposition of charges with solved numericals: Principle of Superposition - create a new page here
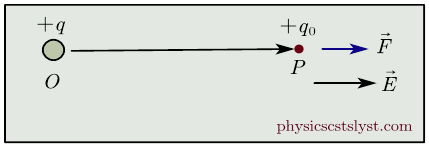
5. Electric Field – Definition and Formula
The electric field at a point is defined as the electrostatic force experienced per unit positive test charge placed at that point.
$$\vec{E} = \frac{\vec{F}}{q_0}$$
where $q_0$ is a small positive test charge.

Electric Field Due to a Point Charge:
$$\vec{E} = \frac{1}{4\pi\varepsilon_0}\frac{q}{r^2}\hat{r}$$
Key Properties:
- Direction is the direction of force on a positive test charge
- Unit: N/C or V/m
- Vector quantity
- Electric field exists even in the absence of a test charge
Electric Field Due to Multiple Charges:
Using superposition principle,
$$\vec{E} = \vec{E}_1 + \vec{E}_2 + \vec{E}_3 + ...$$
👉 Electric field calculation and numerical examples: Electric Field & Calculation of Electric Field
6. Electric Field Due to Continuous Charge Distribution
When electric charge is distributed continuously over a line, surface, or volume, it is described using charge density.
Types of Charge Density:
Linear charge density:
$$\lambda = \frac{dq}{dl} \quad (\text{C/m})$$Surface charge density:
$$\sigma = \frac{dq}{dA} \quad (\text{C/m}^2)$$Volume charge density:
$$\rho = \frac{dq}{dV} \quad (\text{C/m}^3)$$
The electric field due to a continuous charge distribution is obtained by applying the principle of superposition to all charge elements.
General Expression:
$$\vec{E} = \frac{1}{4\pi\varepsilon_0}\int \frac{dq}{r^2}\hat{r}$$
👉 Electric field due to line charge – derivation and applications: Electric Field Due to Line Charge
7. Electric Field Lines – Properties and Patterns
Electric field lines are imaginary curves drawn in such a way that the tangent at any point on the curve gives the direction of the electric field at that point.
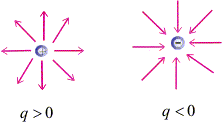
Properties of Electric Field Lines:
- Field lines originate from positive charges and terminate on negative charges
- Field lines never cross each other
- The tangent to a field line at any point gives the direction of electric field at that point
- The number of field lines per unit area (density) is proportional to the magnitude of electric field
- Field lines are perpendicular to the surface of a conductor
- Field lines do not form closed loops
- In a uniform electric field, field lines are parallel and equally spaced
Field Line Patterns:
- Single positive charge: radially outward
- Single negative charge: radially inward
- Electric dipole: emerge from positive, terminate on negative
- Two positive charges: repulsive pattern
👉 Electric field lines – diagrams and important properties: Electric Field Lines
8. Electric Flux – Definition and Formula
Electric flux through a surface is a measure of the number of electric field lines passing through that surface. It gives the total electric field passing through a given area.
Definition:
For a uniform electric field: $$\Phi = \vec{E} \cdot \vec{A} = EA\cos\theta$$
For a non-uniform electric field: $$\Phi = \int \vec{E} \cdot d\vec{A}$$
where:
- Φ = electric flux
- θ = angle between electric field and area vector
- dA = area element with direction along the outward normal
Properties:
- Scalar quantity
- Unit: Nm²/C or Vm
- Can be positive, negative, or zero depending on θ
- Maximum when θ = 0° (field perpendicular to surface)
- Zero when θ = 90° (field parallel to surface)
👉 Electric flux – detailed explanation with examples: Electric Flux
9. Electric Dipole and Dipole Moment
An electric dipole consists of two equal and opposite point charges $+q$ and $-q$ separated by a small distance $2a$.
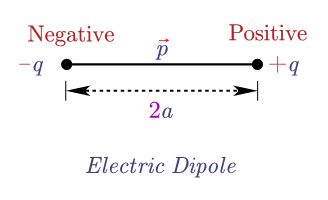
Electric Dipole Moment:
$$\vec{p} = q \cdot 2\vec{a}$$
- Direction: from negative charge to positive charge
- Unit: C m
- Vector quantity
Electric Field of a Dipole (for $r \gg a$):
On axial line:
$$E = \frac{1}{4\pi\varepsilon_0}\frac{2p}{r^3}$$On equatorial line:
$$E = \frac{1}{4\pi\varepsilon_0}\frac{p}{r^3}$$
Torque on a Dipole in Uniform Electric Field:
$$\vec{\tau} = \vec{p} \times \vec{E}$$
Magnitude:
$$\tau = pE\sin\theta$$
- Torque tends to align the dipole with the electric field
👉 Electric dipole field and torque in uniform electric field: Electric Dipole and Dipole Moment
10. Gauss’s Law and Its Applications
Gauss’s law relates the electric flux through a closed surface to the total electric charge enclosed by that surface.
Statement:
The total electric flux through any closed surface is equal to $\frac{1}{\varepsilon_0}$ times the net charge enclosed by the surface.
$$\oint \vec{E}\cdot d\vec{A} = \frac{Q_{\text{enclosed}}}{\varepsilon_0}$$
Key Points:
- The surface used is called a Gaussian surface
- $Q_{\text{enclosed}}$ includes only charges inside the surface
- Electric field $\vec{E}$ is due to all charges (inside and outside)
- Gauss’s law is most useful when the charge distribution has high symmetry
Important Applications (Results Only):
Infinite straight line charge:
$$E = \frac{\lambda}{2\pi\varepsilon_0 r}$$Infinite plane sheet of charge:
$$E = \frac{\sigma}{2\varepsilon_0}$$Uniformly charged spherical shell:
- Outside $(r > R)$:
$$E = \frac{1}{4\pi\varepsilon_0}\frac{Q}{r^2}$$ - Inside $(r < R)$:
$$E = 0$$
- Outside $(r > R)$:
👉 Gauss’s law applications with derivations: Gauss's Law and Applications
Important Formula Sheet
Basic Formulas
Quantization of charge: $$q = ne$$
Coulomb's law: $$F = \frac{1}{4\pi\varepsilon_0}\frac{q_1 q_2}{r^2}$$
Electric field: $$E = \frac{F}{q_0} = \frac{1}{4\pi\varepsilon_0}\frac{q}{r^2}$$
Electric field due to dipole (axial): $$E = \frac{1}{4\pi\varepsilon_0}\frac{2p}{r^3}$$ (for r >> a)
Electric field due to dipole (equatorial): $$E = \frac{1}{4\pi\varepsilon_0}\frac{p}{r^3}$$ (for r >> a)
Electric dipole moment: $$p = q \times 2a$$
Torque on dipole: $$\tau = pE\sin\theta$$
Electric flux: $$\Phi = E \cdot A \cdot \cos\theta$$
Gauss's law: $$\oint \vec{E} \cdot d\vec{A} = \frac{Q}{\varepsilon_0}$$
Charge Density Formulas
Linear charge density: $$\lambda = \frac{q}{l}$$
Surface charge density: $$\sigma = \frac{q}{A}$$
Volume charge density: $$\rho = \frac{q}{V}$$
Constants
- Elementary charge: e = 1.6 × 10⁻¹⁹ C
- Coulomb's constant: k = 9 × 10⁹ Nm²/C²
- Permittivity of free space: ε₀ = 8.854 × 10⁻¹² C²/Nm²
Electric Charges and Fields – One Page Handwritten Formula Sheet (Class 12 Physics)

Weightage and Exam Focus (CBSE Class 12)
Electric Charges and Fields is part of the Electrostatics unit, which carries 10 marks in the Class 12 Physics board examination. From recent CBSE papers, this chapter typically contributes around 4 marks.
Questions from this chapter mainly test:
- Understanding of basic laws
- Application of formulas
- Numerical problem-solving skills
Based on recent exam trends, including the latest board paper, the following topics deserve priority.
Topic-wise Weightage Trend
| Topic | Priority Level | Typical Marks |
|---|---|---|
| Coulomb’s Law | High | 1 mark (MCQ or conceptual) |
| Electric Field & Superposition | High | 3 marks (numerical) |
| Electric Dipole | Medium | 0–1 mark (rotational) |
| Gauss’s Law | Medium–High | 0–1 mark (rotational) |
Note: Not all topics appear every year. CBSE usually rotates questions among Electric Field, Electric Dipole, and Gauss’s Law.
Common Question Pattern
1-mark MCQ:
Often from Coulomb’s law, inverse square dependence, or basic properties of charges.3-mark Numerical:
Commonly based on electric field due to point charges using the superposition principle.
In recent papers, this chapter has appeared as a combination of one MCQ and one numerical, carrying a total of 4 marks.
How Students Should Use This Information
- Master Coulomb’s law formulas and concepts
- Practise electric field numericals thoroughly
- Revise dipole and Gauss’s law results, even if they are not asked every year
This approach ensures efficient preparation without ignoring important but rotational topics.
Common Mistakes and Exam Tips (Electric Charges and Fields)
Students often lose marks in this chapter due to conceptual and formula-based mistakes. Some common points to keep in mind are:
- Force and electric field are different quantities: Force depends on the test charge, whereas electric field does not. Do not confuse $F$ with $E$.
- Vector nature of electric field is often ignored. Direction must be mentioned, especially in questions involving multiple charges.
- Gauss’s law should be applied only when sufficient symmetry exists. It cannot be used to find electric field for arbitrary charge distributions.
- While using Coulomb’s law, ensure charges are treated as point charges and are at rest.
- For an electric dipole, remember that the electric field varies as $1/r^3$, not $1/r^2$.
- Inside a uniformly charged spherical shell, the electric field is zero, a frequently tested concept.
- Always check units and powers of distance while solving numericals.
Practice Section – CBSE and Competitive Exam Questions
Master this chapter through comprehensive practice:
👉 Conceptual Questions: Electric Charges and Fields Questions and Answers
👉 Important Exam Questions: Electrostatics Important Questions for Class 12
👉 MCQs: Electrostatics Multiple Choice Questions
👉 Numerical Problems: Electrostatics Numericals
How to Study This Chapter
- Start with the short notes on this page to understand all key concepts quickly
- Click individual topics for detailed theory, derivations, and solved examples
- Solve numericals and MCQs after understanding each concept thoroughly
- Revise formulas from this page regularly, especially before exams
- Practice previous year questions to understand exam patterns and important topics
This systematic approach will help you build a strong foundation in electrostatics and excel in your Class 12 board exams and competitive examinations.
Revision and Concept Strengthening
For a complete and structured revision of the chapter, refer to our Electrostatics Summary Notes for Class 12 Physics. It covers all important definitions, formulas, standard results and key concepts from Coulomb’s law, electric field, electric dipole and Gauss’s law in a concise format useful for quick revision before exams.
To deepen your understanding of conductor behaviour and symmetry-based field calculations, study Electric Field Due to a Charged Conductor, which explains electric field inside and outside conductors and its connection with Gauss’s law applications.
Build strong numerical problem-solving skills using our guide on Solving Electric Force and Electric Field Problems Step-by-Step. This resource helps you apply Coulomb’s law, superposition principle and vector methods correctly in board and competitive exam questions.
Board and Competitive Exam Practice
For descriptive and conceptual practice, go through Electric Charges and Fields Questions and Answers and CBSE Class 12 Electrostatics Important Questions, carefully selected according to recent exam trends.
Strengthen your preparation further with Electrostatics Board Exam Practice Questions and attempt the Electric Charges and Fields MCQ Online Test for objective practice useful in CBSE, JEE and NEET examinations.
